Εργασία για το μάθημα Μηχανική Μάθηση

Author

Κώστας Κούδας

Published

February 15, 2026

1 Υπόβαθρο

# Για την αισθητική παρουσίαση
knitr::opts_chunk$set(echo = TRUE)
if(!require(kableExtra)){
  install.packages("kableExtra")
  library(kableExtra)
}
Loading required package: kableExtra

Η παρούσα σελίδα είναι η υλοποίηση της εργασίας του μαθήματος Μηχανική Μάθηση του Τμήματος Πληροφορικής του Ιονίου Πανεπιστημίου. Διαδάσκων καθηγητής Κώστας Γιαννάκης. Ακολουθεί η εκφώνησή της:

# Πακέτα

# Για τα γραφήματα που θα χρειαστούν
if(!require(ggplot2)){
  install.packages("ggplot2")
  library(ggplot2)
}
Loading required package: ggplot2
# Για ιστόγραμμα σε συνδυασμό με θηκόγραμμα
if(!require(packHV)){
    install.packages("packHV")
    library(packHV)
}
Loading required package: packHV
Loading required package: survival
# Για grid-plot
if(!require(GGally)){
    install.packages("GGally")
    library(GGally)
}
Loading required package: GGally
# Για δέντρα αποφάσεων
if(!require(rpart)){
    install.packages("rpart")
    library(rpart)
}
Loading required package: rpart
if(!require(rpart.plot)){
    install.packages("rpart.plot")
    library(rpart.plot)
}
Loading required package: rpart.plot
if(!require(caret)){
    install.packages("caret")
    library(caret)
}
Loading required package: caret
Loading required package: lattice

Attaching package: 'caret'
The following object is masked from 'package:survival':

    cluster
if(!require(tidymodels)){
    install.packages("tidymodels")
    library(tidymodels)
}
Loading required package: tidymodels
── Attaching packages ────────────────────────────────────── tidymodels 1.4.1 ──
✔ broom        1.0.11     ✔ rsample      1.3.1 
✔ dials        1.4.2      ✔ tailor       0.1.0 
✔ dplyr        1.1.4      ✔ tidyr        1.3.1 
✔ infer        1.0.9      ✔ tune         2.0.1 
✔ modeldata    1.5.1      ✔ workflows    1.3.0 
✔ parsnip      1.4.0      ✔ workflowsets 1.1.1 
✔ purrr        1.0.4      ✔ yardstick    1.3.2 
✔ recipes      1.3.1      
── Conflicts ───────────────────────────────────────── tidymodels_conflicts() ──
✖ rsample::calibration()   masks caret::calibration()
✖ dplyr::desc()            masks packHV::desc()
✖ purrr::discard()         masks scales::discard()
✖ dplyr::filter()          masks stats::filter()
✖ dplyr::group_rows()      masks kableExtra::group_rows()
✖ dplyr::lag()             masks stats::lag()
✖ purrr::lift()            masks caret::lift()
✖ yardstick::precision()   masks caret::precision()
✖ dials::prune()           masks rpart::prune()
✖ yardstick::recall()      masks caret::recall()
✖ yardstick::sensitivity() masks caret::sensitivity()
✖ yardstick::specificity() masks caret::specificity()
✖ recipes::step()          masks stats::step()
if(!require(class)){
    install.packages("class")
    library(class)
}
Loading required package: class
if(!require(nnet)){# για τα νευρωνικά δίκτυα
    install.packages("nnet")
    library(nnet)
}
Loading required package: nnet
if(!require(factoextra)){# για k-means
    install.packages("factoextra")
    library(factoextra)
}
Loading required package: factoextra
Welcome! Want to learn more? See two factoextra-related books at https://goo.gl/ve3WBa
if(!require(cluster)){# για elbow method
    install.packages("cluster")
    library(cluster)
}
Loading required package: cluster
if(!require(plotly)){
    install.packages("plotly")
    library(plotly)
}
Loading required package: plotly

Attaching package: 'plotly'
The following object is masked from 'package:ggplot2':

    last_plot
The following object is masked from 'package:stats':

    filter
The following object is masked from 'package:graphics':

    layout
if(!require(factoextra)){
    install.packages("factoextra")
    library(factoextra)
}

if(!require(dbscan)){# για dbscan
    install.packages("dbscan")
    library(dbscan)
}
Loading required package: dbscan

Attaching package: 'dbscan'
The following object is masked from 'package:stats':

    as.dendrogram
if(!require(ranger)){# για αυτόματο random forest
    install.packages("ranger")
    library(ranger)
}
Loading required package: ranger

2 Εισαγωγή και παρουσίαση δεδομένων

Αρχικά καθαρίζουμε τη μνήμη της R.

rm(list = ls())

Ακολούθως εισάγουμε τα δεδομένα μας.

mushrooms <- read.csv("mushrooms_clean.csv",
                     header = TRUE, sep = ",")

Καθόσον ο Α.Μ. του γράφοντος είναι inf2021102 οι τιμές των δεδομένων αλλοιώνονται, σύμφωνα με τις οδηγίες του διδάσκοντος ως ακολούθως:

# Ο Α.Μ.
student_id <- "inf2021102"
# Αφαιρούμε το τμήμα "inf" του Α.Μ.
student_id <- as.numeric(gsub("[^0-9]", "", student_id))
# Η βάση της τυχαιότητας
set.seed(student_id)
# Συλλέγουμε κάποιες τυχαίες γραμμές από το mushrooms
sampled_mushrooms <- mushrooms[sample(nrow(mushrooms), 15000), ]
# Συλλέγουμε κάποιες τυχαίες στήλες από το mushrooms
sampled_mushrooms <- sampled_mushrooms[, c(1,sample(2:ncol(sampled_mushrooms), 9))]

Ας δούμε αν όλα πάνε καλά. Καταρχάς, θα πρέπει να έχουμε 15000 γραμμές. Γράφουμε:

nrow(sampled_mushrooms) # 15000 γραμμές;
[1] 15000

Όλα βαίνουν καλώς, οπότε προχωράμε στον έλεγχο των στηλών. Θα πρέπει να είναι 10. Γράφουμε:

ncol(sampled_mushrooms) # 10 στήλες;
[1] 10

Η διαδικασία πρέπει να είναι εντάξει, οπότε ας ρίξουμε μια ματιά στα δεδομένα μας. Επειδή ο πίνακας ήταν πλατύς, θεωρήθηκε χρήσιμο να παρουσιαστεί με τη βοήθεια των συναρτήσεων kable() και kable_styling.

knitr::kable(head(sampled_mushrooms)) %>%
  kable_styling("striped", full_width = T) %>%
  scroll_box(width = "100%", height = "max-content")
class Feature_7 Feature_11 Feature_6 Feature_2 Feature_10 Feature_8 Feature_1 Feature_5 Feature_4
40828 p 25.02 u 14.69 x d y 12.49 o FALSE
26825 p 26.70 a 6.68 f d w 18.91 w TRUE
9321 e 3.14 a 4.92 b g y 3.04 w FALSE
15313 p 12.79 a 4.35 x d w 5.11 w TRUE
3074 e 20.14 u 27.41 f d n 18.98 w FALSE
38361 p 5.18 a 5.05 x d e 3.54 e FALSE

Ας ρίξουμε μια πιο προσεκτική ματιά στον πίνακα.

# Μια αναλυτικότερη εικόνα των δεδομένων μας
str(sampled_mushrooms)
'data.frame':   15000 obs. of  10 variables:
 $ class     : chr  "p" "p" "e" "p" ...
 $ Feature_7 : num  25.02 26.7 3.14 12.79 20.14 ...
 $ Feature_11: chr  "u" "a" "a" "a" ...
 $ Feature_6 : num  14.69 6.68 4.92 4.35 27.41 ...
 $ Feature_2 : chr  "x" "f" "b" "x" ...
 $ Feature_10: chr  "d" "d" "g" "d" ...
 $ Feature_8 : chr  "y" "w" "y" "w" ...
 $ Feature_1 : num  12.49 18.91 3.04 5.11 18.98 ...
 $ Feature_5 : chr  "o" "w" "w" "w" ...
 $ Feature_4 : logi  FALSE TRUE FALSE TRUE FALSE FALSE ...

Βλέπουμε ότι:

  • οι μεταβλητές class, Feature_11, Feature_2, Feature_10, Feature_8 και Feature_5 είναι απλές συμβολοσειρές,

  • οι μεταβλητές Feature_7, Feature_6 και Feature_1 είναι αριθμητικές τιμές (όχι απαραιτήτως ακέραιες),

  • η μεταβλητή Feature_4 είναι λογική.

Ας κάνουμε λίγο βαθύτερη την πρώτη αυτή παρατήρηση των δεδομένων μας.

# Μια αναλυτικότερη εικόνα των δεδομένων μας
summary(sampled_mushrooms)
    class             Feature_7       Feature_11          Feature_6     
 Length:15000       Min.   :  0.00   Length:15000       Min.   : 0.000  
 Class :character   1st Qu.:  5.17   Class :character   1st Qu.: 4.630  
 Mode  :character   Median : 10.26   Mode  :character   Median : 5.960  
                    Mean   : 12.23                      Mean   : 6.577  
                    3rd Qu.: 16.87                      3rd Qu.: 7.760  
                    Max.   :102.48                      Max.   :32.430  
  Feature_2          Feature_10         Feature_8           Feature_1     
 Length:15000       Length:15000       Length:15000       Min.   : 0.440  
 Class :character   Class :character   Class :character   1st Qu.: 3.470  
 Mode  :character   Mode  :character   Mode  :character   Median : 5.900  
                                                          Mean   : 6.753  
                                                          3rd Qu.: 8.600  
                                                          Max.   :62.340  
  Feature_5         Feature_4      
 Length:15000       Mode :logical  
 Class :character   FALSE:12362    
 Mode  :character   TRUE :2638

Μεταφράζουμε σε απλά ελληνικά τον πίνακα παρακάτω. Συγχρόνως οπτικοποιούμε τα εν λόγω αποτελέσματα.

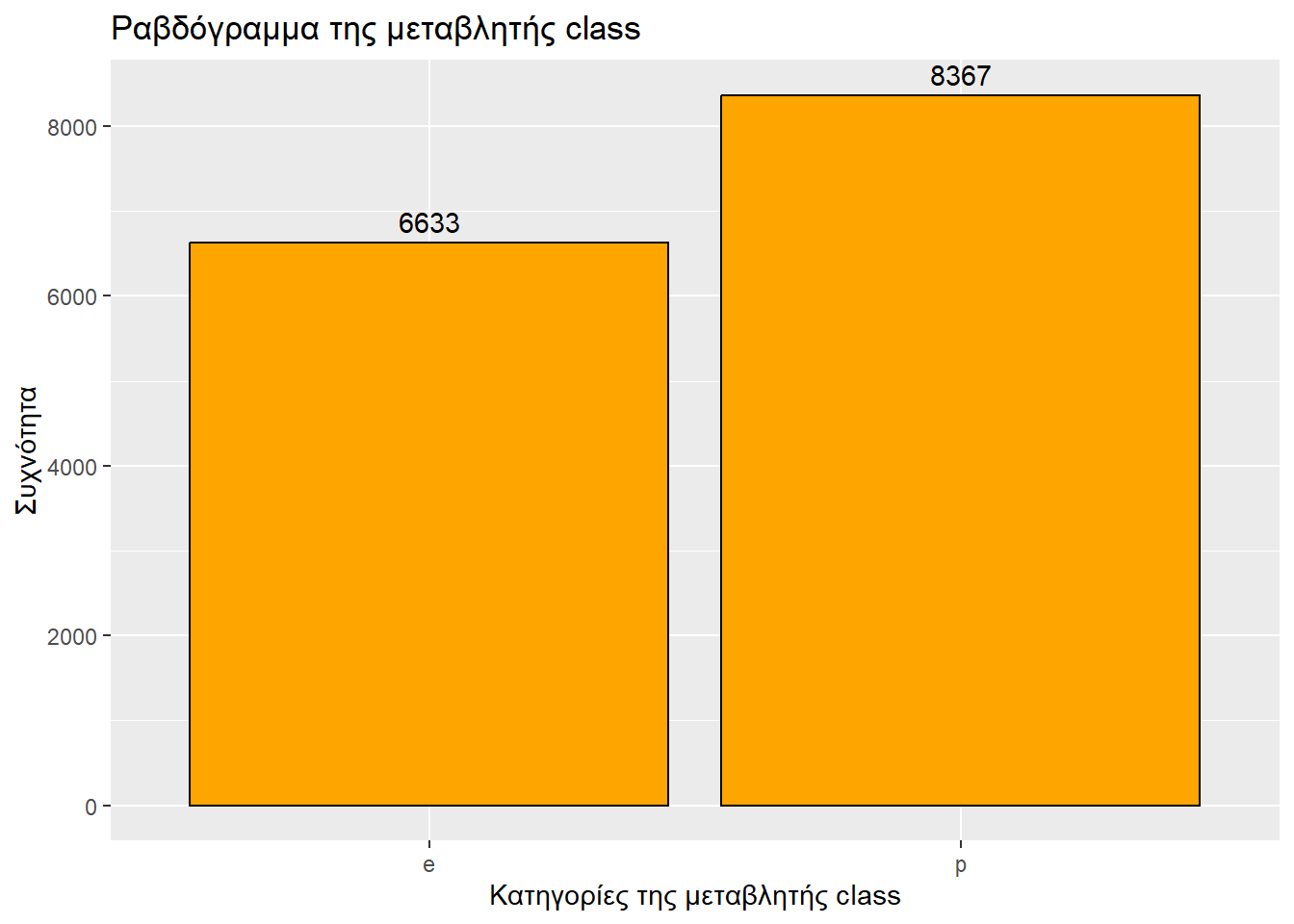
  • Τύπος μεταβλητής: κατηγορική

  • Αριθμός καταχωρήσεων: 15000

ggplot(sampled_mushrooms, aes(x = class)) +
  geom_bar(fill = "orange", color = "black") + # Το ραβδόγραμμα
  labs(
    title = "Ραβδόγραμμα της μεταβλητής class",
    x = "Κατηγορίες της μεταβλητής class",
    y = "Συχνότητα"
  ) +
  geom_text( # Για ετικέτες συχνοτήτων
  stat = 'count',  
  aes(label = after_stat(count)),
  vjust = -0.5
)

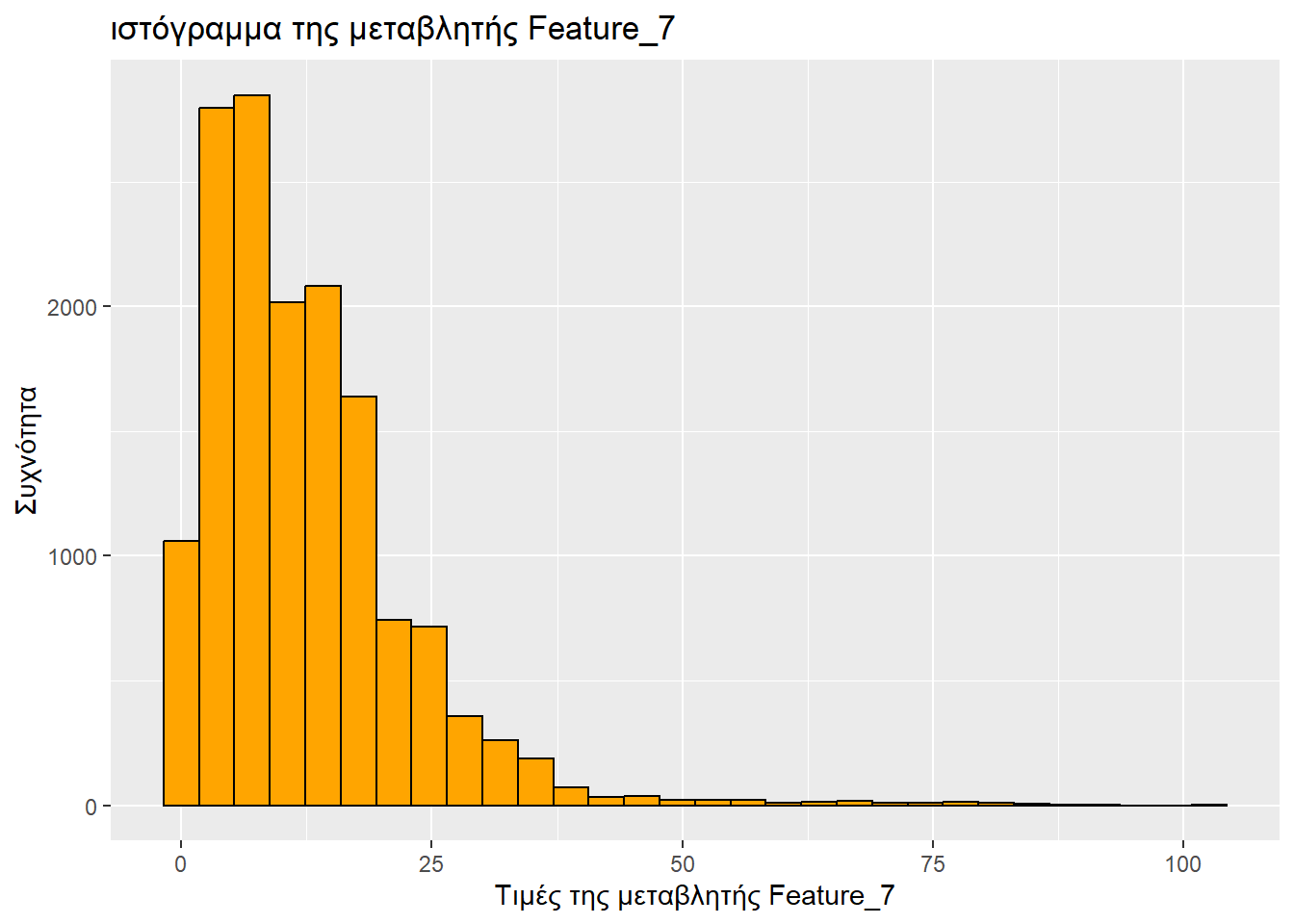
  • Τύπος μεταβλητής: αριθμητική

  • Ελάχιστη τιμή: 0

  • 1ο τεταρτημόριο: 5.17

  • Διάμεσος: 10.26

  • Μέση τιμή: 12.226284

  • 3ο τεταρτημόριο: 16.87

  • Μέγιστη τιμή: 102.48

ggplot(sampled_mushrooms, aes(x = Feature_7)) +
  # Το ιστόγραμμα
  geom_histogram(bins = 30, fill = "orange", color = "black") + # Το bins πήγε γιατί έβγαζε μήνυμα «`stat_bin()` using `bins = 30`. Pick better value with `binwidth`.»
  labs(
    title = "ιστόγραμμα της μεταβλητής Feature_7",
    x = "Τιμές της μεταβλητής Feature_7",
    y = "Συχνότητα"
  )

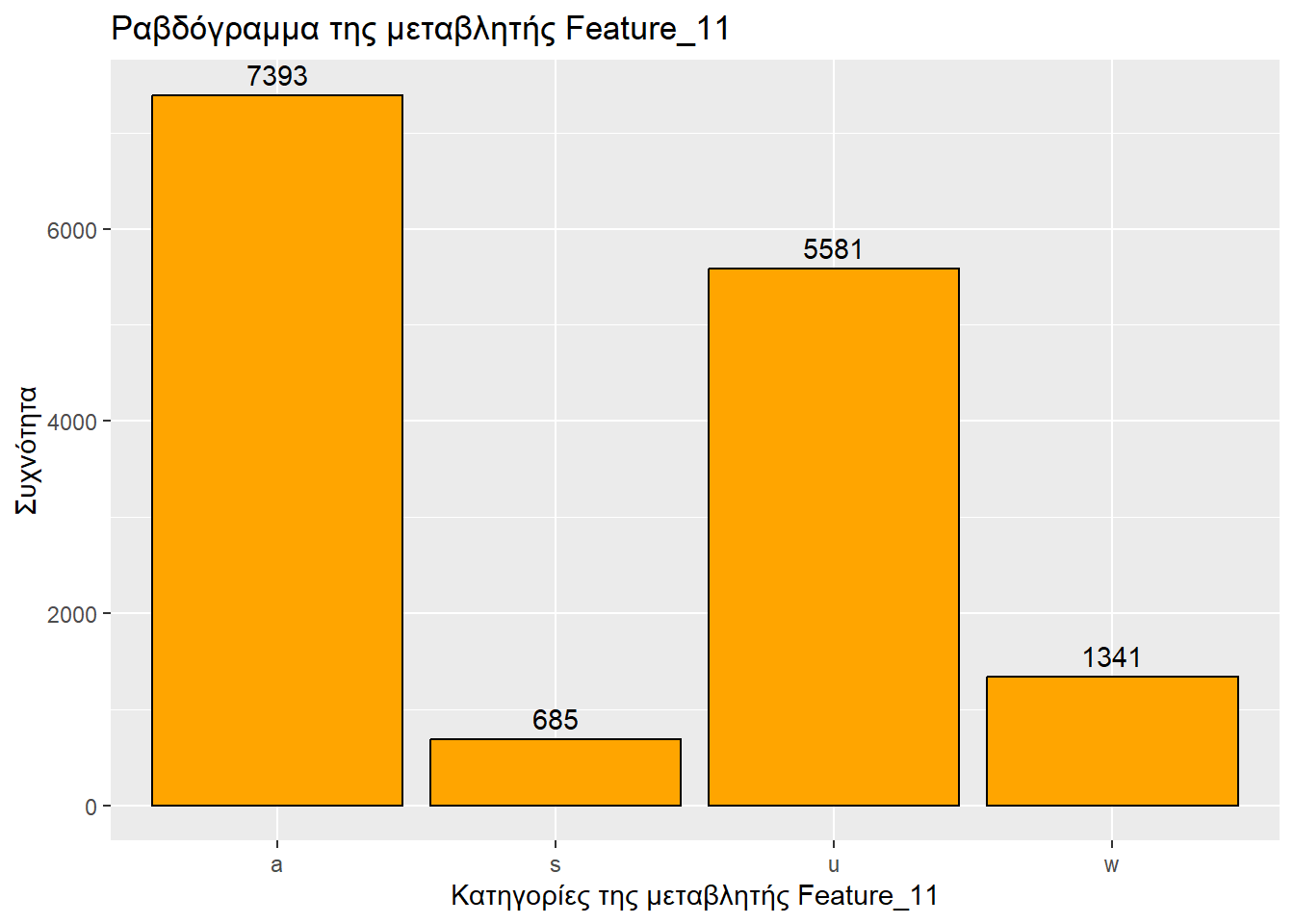
  • Τύπος μεταβλητής: κατηγορική

  • Αριθμός καταχωρήσεων: 15000

ggplot(sampled_mushrooms, aes(x = Feature_11)) +
  geom_bar(fill = "orange", color = "black") + # Το ραβδόγραμμα
  labs(
    title = "Ραβδόγραμμα της μεταβλητής Feature_11",
    x = "Κατηγορίες της μεταβλητής Feature_11",
    y = "Συχνότητα"
  ) +
  geom_text( # Για ετικέτες συχνοτήτων
  stat = 'count',  
  aes(label = after_stat(count)),
  vjust = -0.5
)

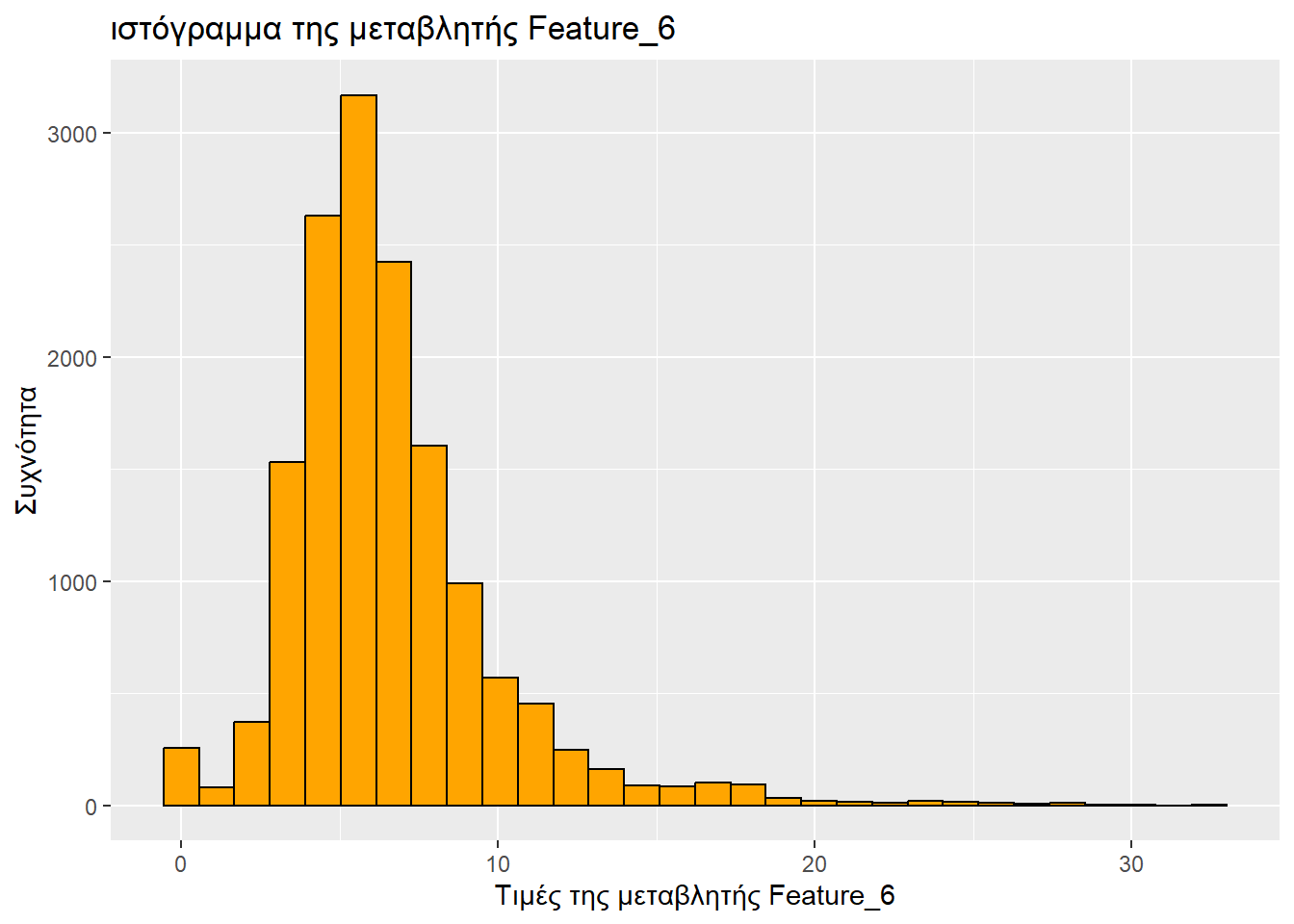
  • Τύπος μεταβλητής: αριθμητική

  • Ελάχιστη τιμή: 0

  • 1ο τεταρτημόριο: 4.63

  • Διάμεσος: 5.96

  • Μέση τιμή: 6.5773807

  • 3ο τεταρτημόριο: 7.76

  • Μέγιστη τιμή: 32.43

ggplot(sampled_mushrooms, aes(x = Feature_6)) +
  # Το ιστόγραμμα
  geom_histogram(bins = 30, fill = "orange", color = "black") + # Το bins πήγε γιατί έβγαζε μήνυμα «`stat_bin()` using `bins = 30`. Pick better value with `binwidth`.»
  labs(
    title = "ιστόγραμμα της μεταβλητής Feature_6",
    x = "Τιμές της μεταβλητής Feature_6",
    y = "Συχνότητα"
  )

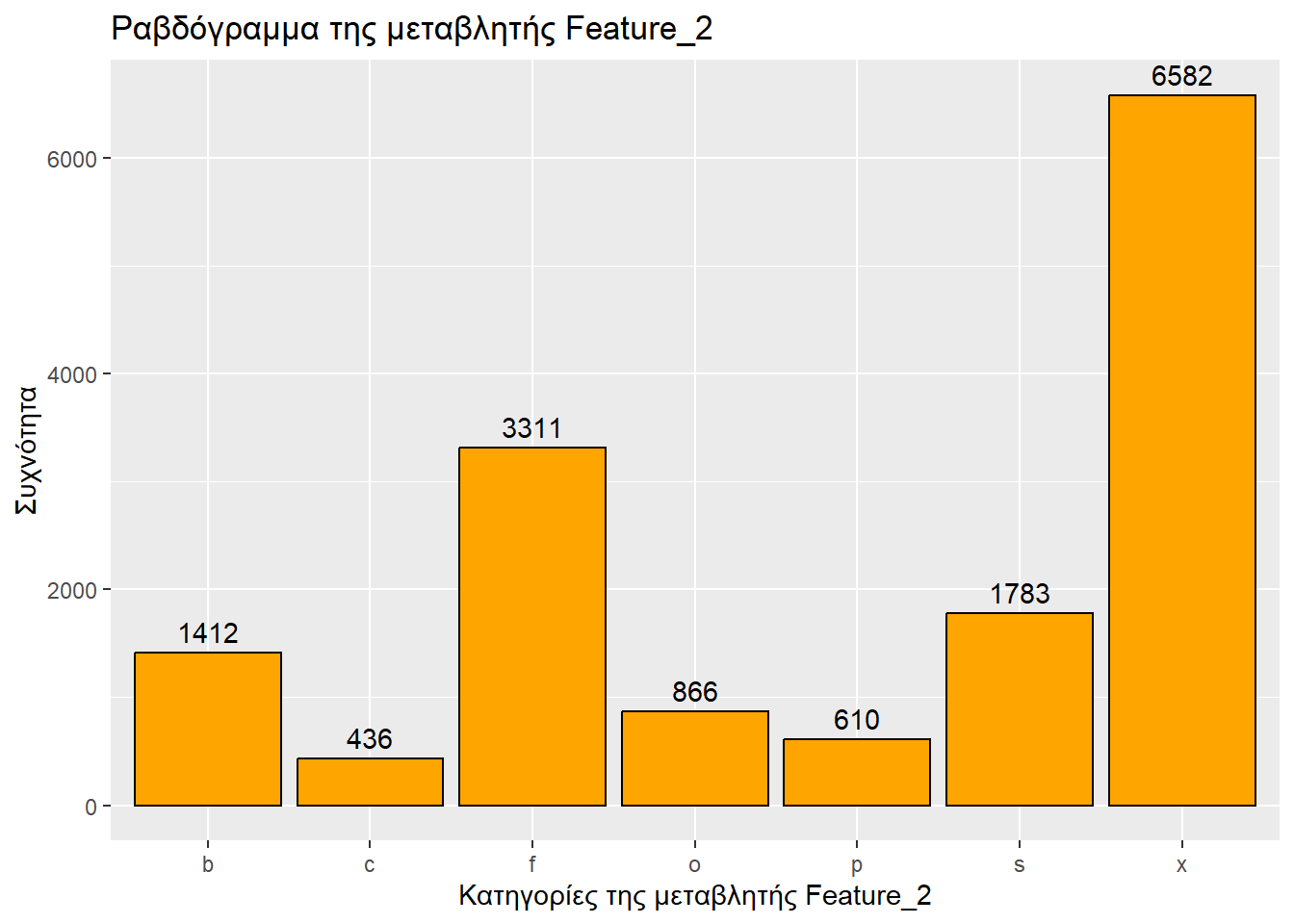
  • Τύπος μεταβλητής: κατηγορική

  • Αριθμός καταχωρήσεων: 15000

ggplot(sampled_mushrooms, aes(x = Feature_2)) +
  geom_bar(fill = "orange", color = "black") + # Το ραβδόγραμμα
  labs(
    title = "Ραβδόγραμμα της μεταβλητής Feature_2",
    x = "Κατηγορίες της μεταβλητής Feature_2",
    y = "Συχνότητα"
  ) +
  geom_text( # Για ετικέτες συχνοτήτων
  stat = 'count',  
  aes(label = after_stat(count)),
  vjust = -0.5
)

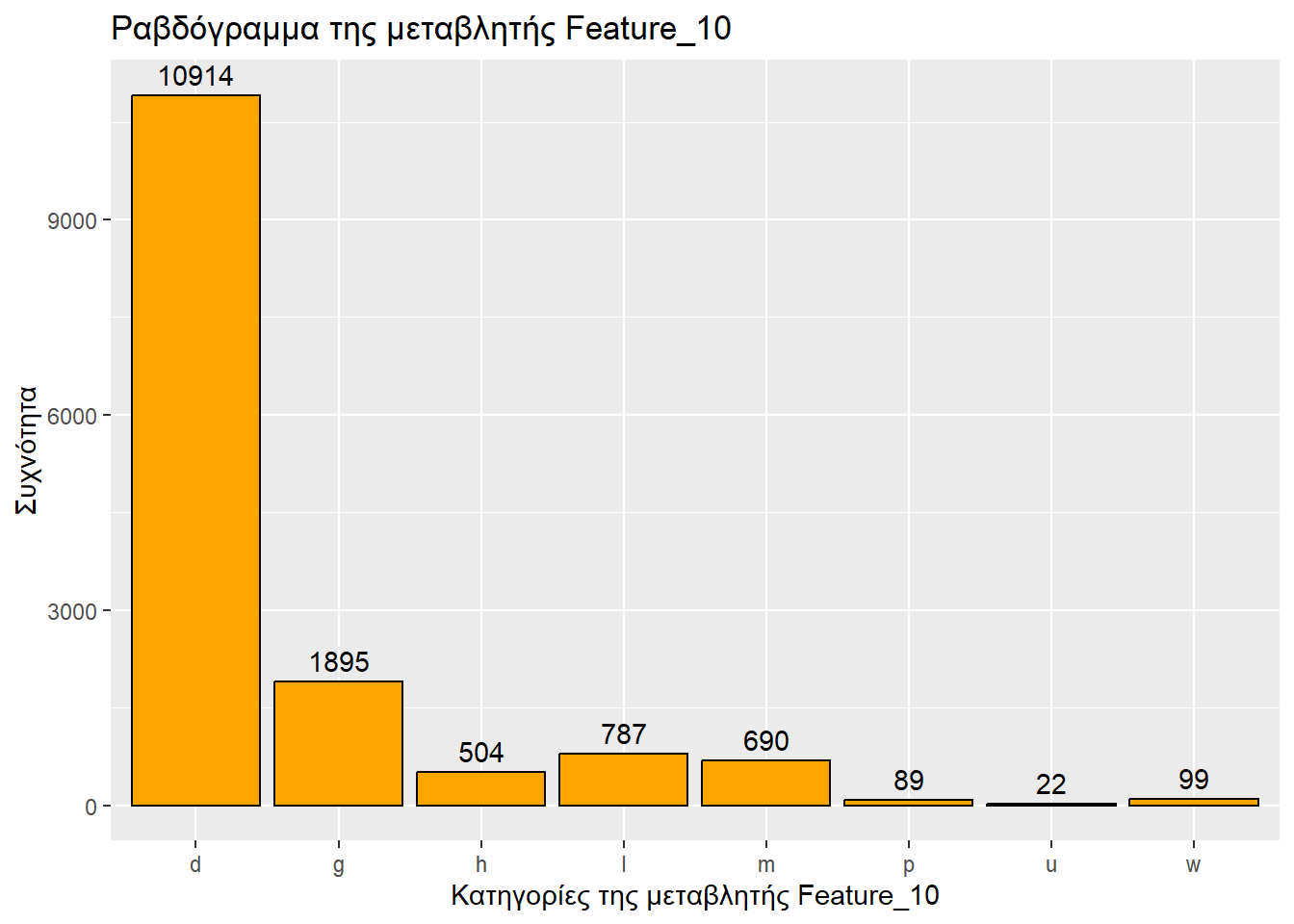
  • Τύπος μεταβλητής: κατηγορική

  • Αριθμός καταχωρήσεων: 15000

ggplot(sampled_mushrooms, aes(x = Feature_10)) +
  geom_bar(fill = "orange", color = "black") + # Το ραβδόγραμμα
  labs(
    title = "Ραβδόγραμμα της μεταβλητής Feature_10",
    x = "Κατηγορίες της μεταβλητής Feature_10",
    y = "Συχνότητα"
  ) +
  geom_text( # Για ετικέτες συχνοτήτων
  stat = 'count',  
  aes(label = after_stat(count)),
  vjust = -0.5
)

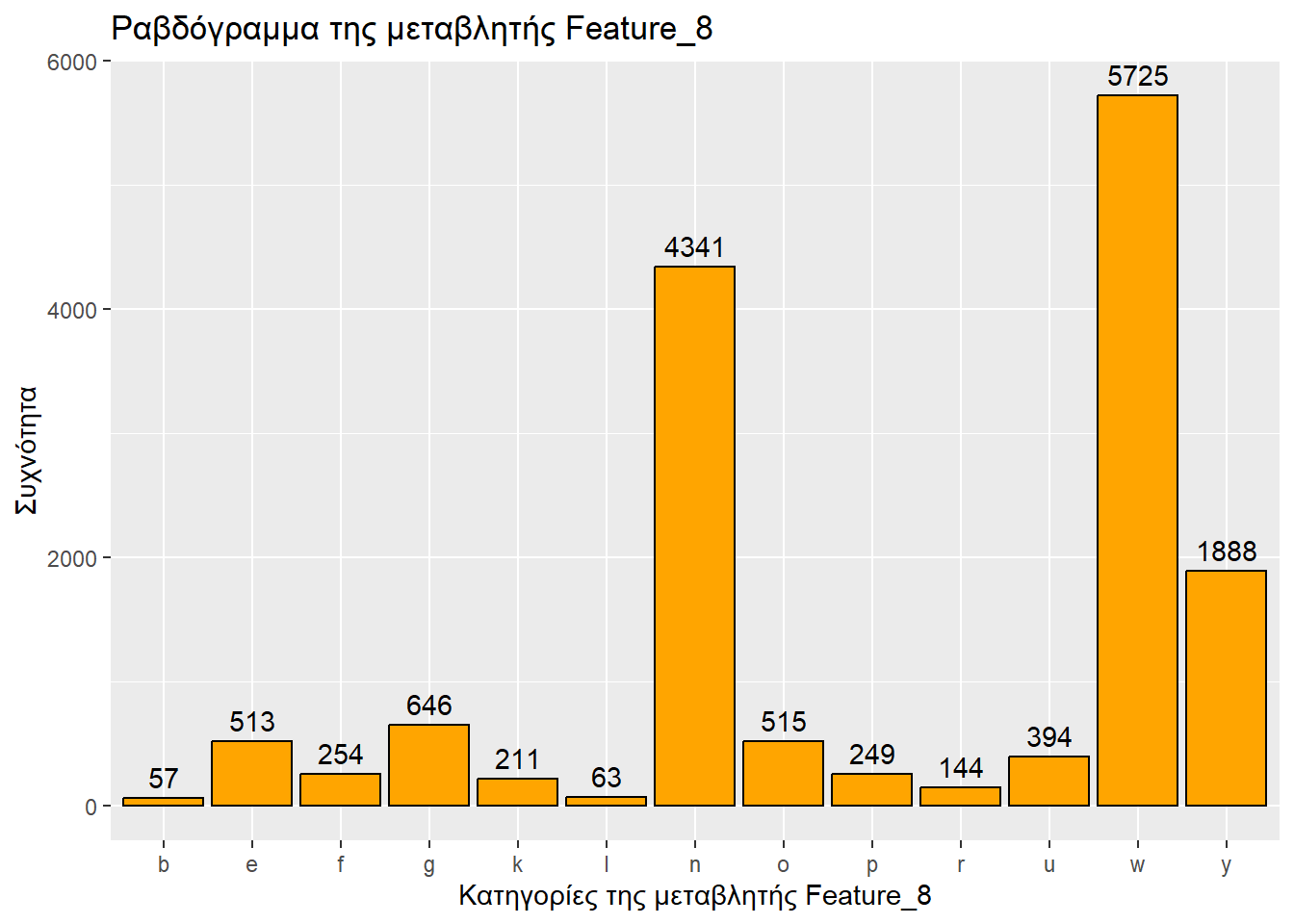
  • Τύπος μεταβλητής: κατηγορική

  • Αριθμός καταχωρήσεων: 15000

ggplot(sampled_mushrooms, aes(x = Feature_8)) +
  geom_bar(fill = "orange", color = "black") + # Το ραβδόγραμμα
  labs(
    title = "Ραβδόγραμμα της μεταβλητής Feature_8",
    x = "Κατηγορίες της μεταβλητής Feature_8",
    y = "Συχνότητα"
  ) +
  geom_text( # Για ετικέτες συχνοτήτων
  stat = 'count',  
  aes(label = after_stat(count)),
  vjust = -0.5
)

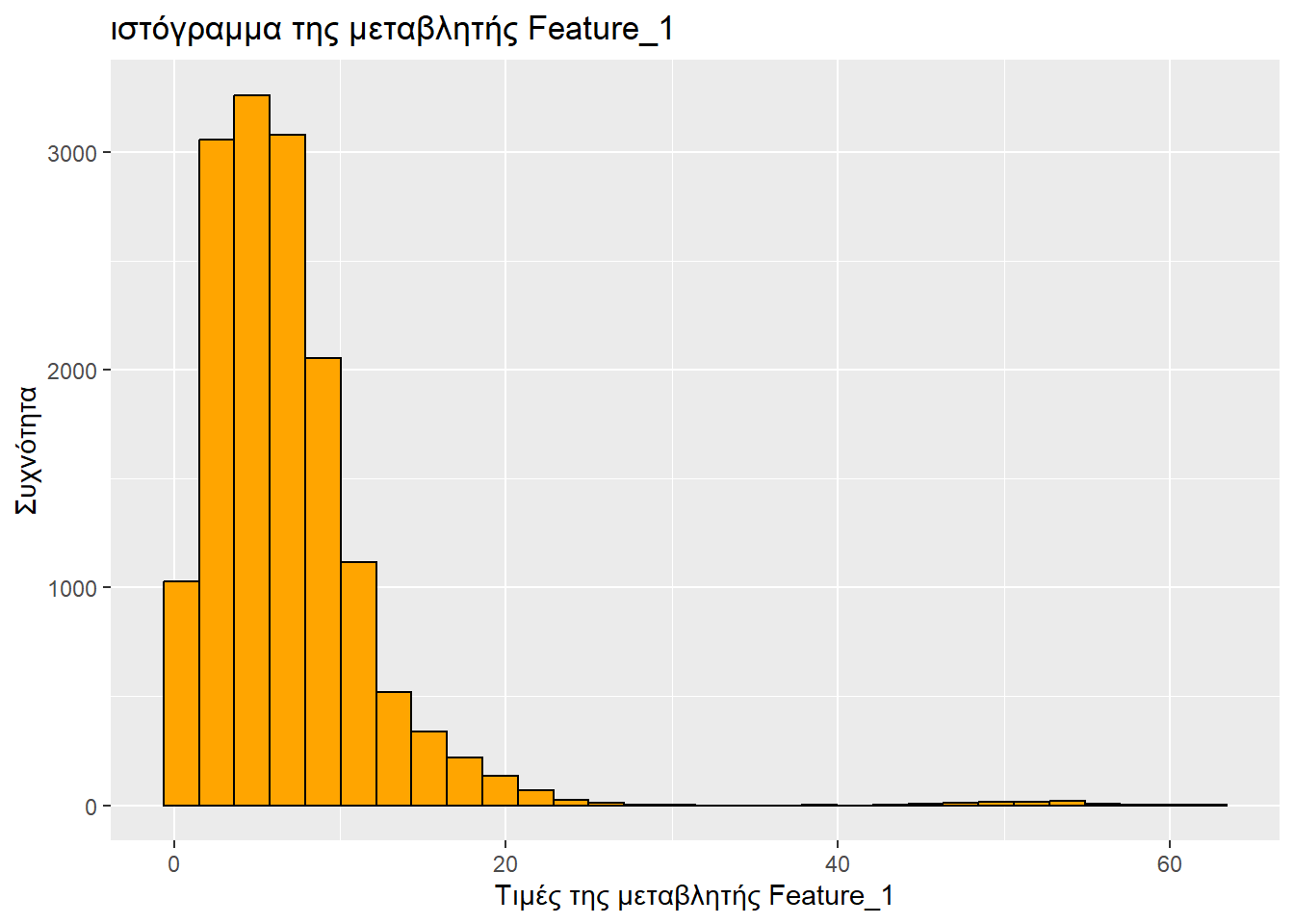
  • Τύπος μεταβλητής: αριθμητική

  • Ελάχιστη τιμή: 0.44

  • 1ο τεταρτημόριο: 3.47

  • Διάμεσος: 5.9

  • Μέση τιμή: 6.753178

  • 3ο τεταρτημόριο: 8.6

  • Μέγιστη τιμή: 62.34

ggplot(sampled_mushrooms, aes(x = Feature_1)) +
  # Το ιστόγραμμα
  geom_histogram(bins = 30, fill = "orange", color = "black") + # Το bins πήγε γιατί έβγαζε μήνυμα «`stat_bin()` using `bins = 30`. Pick better value with `binwidth`.»
  labs(
    title = "ιστόγραμμα της μεταβλητής Feature_1",
    x = "Τιμές της μεταβλητής Feature_1",
    y = "Συχνότητα"
  )

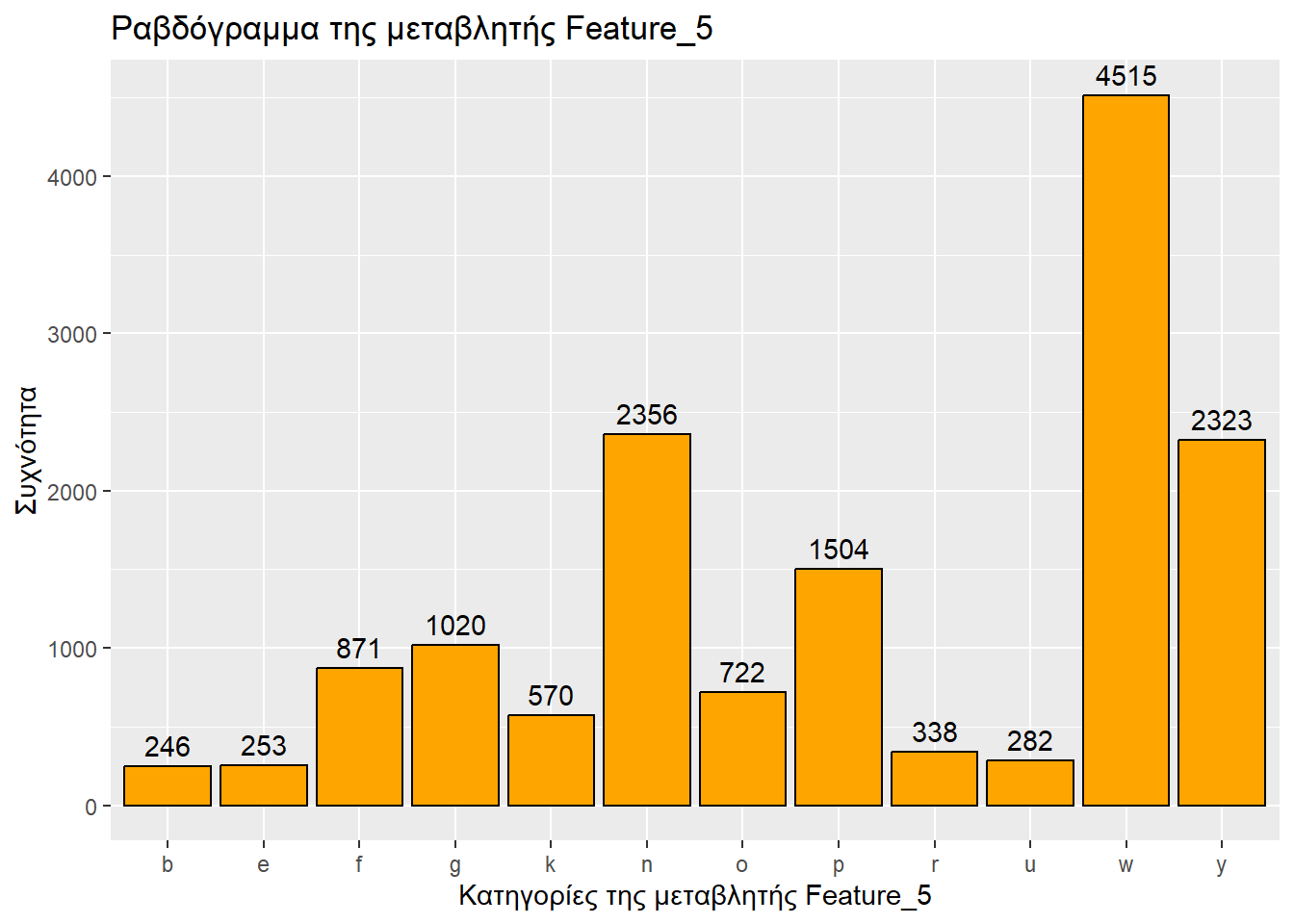
  • Τύπος μεταβλητής: κατηγορική

  • Αριθμός καταχωρήσεων: 15000

ggplot(sampled_mushrooms, aes(x = Feature_5)) +
  geom_bar(fill = "orange", color = "black") + # Το ραβδόγραμμα
  labs(
    title = "Ραβδόγραμμα της μεταβλητής Feature_5",
    x = "Κατηγορίες της μεταβλητής Feature_5",
    y = "Συχνότητα"
  ) +
  geom_text( # Για ετικέτες συχνοτήτων
  stat = 'count',  
  aes(label = after_stat(count)),
  vjust = -0.5
)

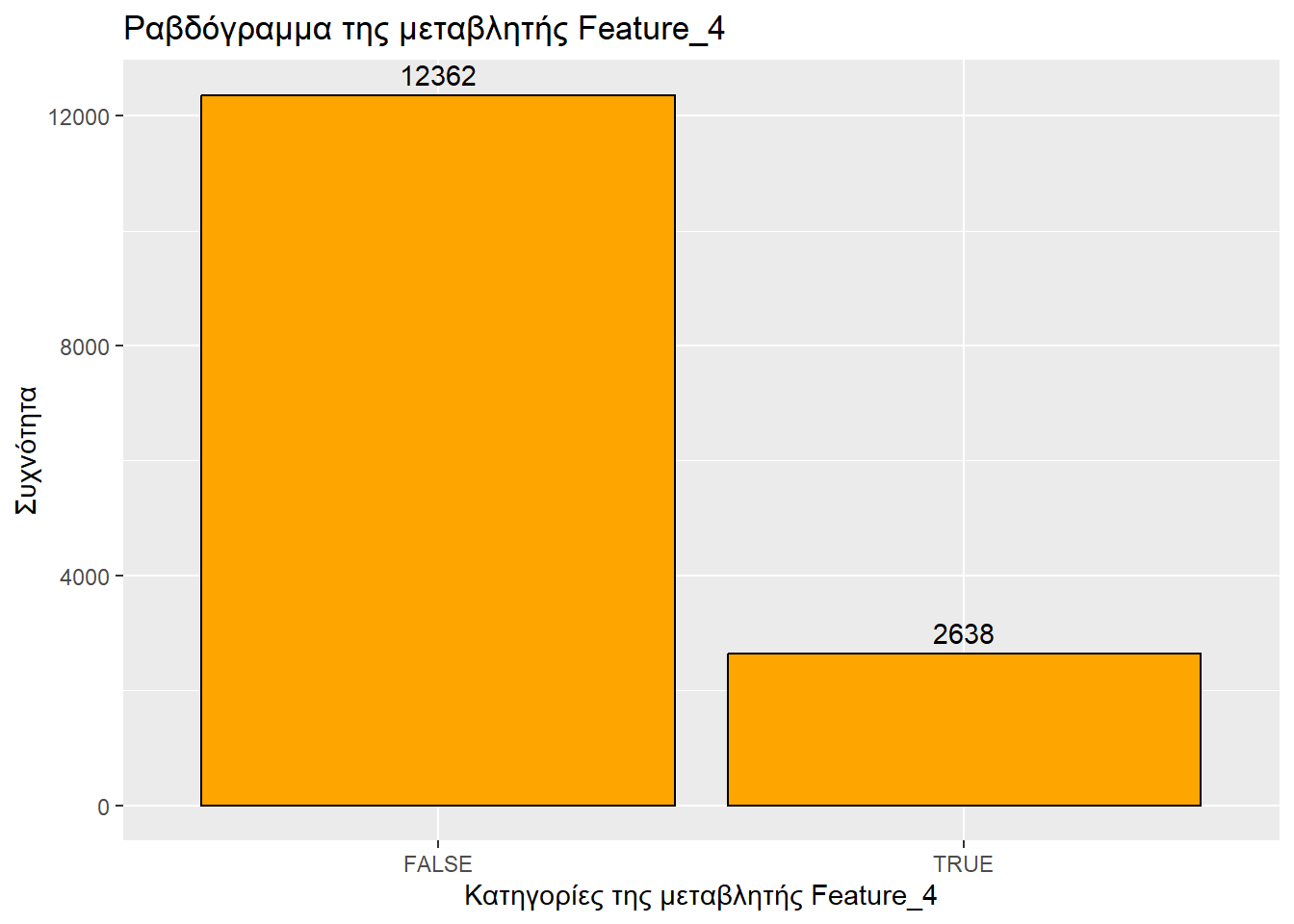
  • Τύπος μεταβλητής: λογική

  • Αριθμός από «Σωστό»: 2638

  • Αριθμός από «Λάθος»: 12362

ggplot(sampled_mushrooms, aes(x = Feature_4)) +
  geom_bar(fill = "orange", color = "black") + # Το ραβδόγραμμα
  labs(
    title = "Ραβδόγραμμα της μεταβλητής Feature_4",
    x = "Κατηγορίες της μεταβλητής Feature_4",
    y = "Συχνότητα"
  ) +
  geom_text( # Για ετικέτες συχνοτήτων
  stat = 'count',  
  aes(label = after_stat(count)),
  vjust = -0.5
)

3 Συνολική προεπεξεργασία δεδομένων

Στο σημείο αυτό παρατηρούμε πως οι κατηγορικές μεταβλητές class, Feature_11, Feature_2, Feature_10, Feature_8 και Feature_5 δεν είναι τελικά απλές συμβολοσειρές. Το μικρό πληθος διαφορετικών τιμών, όπως και η ανάγκη να τις παραστήσουμε σε ραβδογράμματα υποδεικνύουν ότι είναι παράγοντες. Συνεπώς θα κάνουμε και την ανάλογη τροποποίηση στο αρχικό μας dataframe.

# Οι κατηγορικές μας
categorical_cols <- c("class", "Feature_11", "Feature_2", "Feature_10", "Feature_8", "Feature_5")

# Εφαρμόζουμε τη συνάρτηση as.factor σε κάθε μία τους
sampled_mushrooms[, categorical_cols] <- lapply(
  sampled_mushrooms[, categorical_cols], 
  as.factor
)

Πριν προχωρήσουμε, ας ελέγξουμε αν όλα βαίνουν καλώς.

# Έχουν αλλάξει όντως σε factor οι μεταβλητές;
str(sampled_mushrooms)
'data.frame':   15000 obs. of  10 variables:
 $ class     : Factor w/ 2 levels "e","p": 2 2 1 2 1 2 2 1 1 2 ...
 $ Feature_7 : num  25.02 26.7 3.14 12.79 20.14 ...
 $ Feature_11: Factor w/ 4 levels "a","s","u","w": 3 1 1 1 3 1 1 2 1 3 ...
 $ Feature_6 : num  14.69 6.68 4.92 4.35 27.41 ...
 $ Feature_2 : Factor w/ 7 levels "b","c","f","o",..: 7 3 1 7 3 7 1 4 6 1 ...
 $ Feature_10: Factor w/ 8 levels "d","g","h","l",..: 1 1 2 1 1 1 2 1 4 5 ...
 $ Feature_8 : Factor w/ 13 levels "b","e","f","g",..: 13 12 13 12 7 2 7 5 12 7 ...
 $ Feature_1 : num  12.49 18.91 3.04 5.11 18.98 ...
 $ Feature_5 : Factor w/ 12 levels "b","e","f","g",..: 7 11 11 11 11 2 6 12 11 4 ...
 $ Feature_4 : logi  FALSE TRUE FALSE TRUE FALSE FALSE ...
# Παρατηρούμε τις διαφορές της σύνοψης στις εν λόγω μεταβλητές
summary(sampled_mushrooms[, categorical_cols])
 class    Feature_11 Feature_2   Feature_10      Feature_8      Feature_5   
 e:6633   a:7393     b:1412    d      :10914   w      :5725   w      :4515  
 p:8367   s: 685     c: 436    g      : 1895   n      :4341   n      :2356  
          u:5581     f:3311    l      :  787   y      :1888   y      :2323  
          w:1341     o: 866    m      :  690   g      : 646   p      :1504  
                     p: 610    h      :  504   o      : 515   g      :1020  
                     s:1783    w      :   99   e      : 513   f      : 871  
                     x:6582    (Other):  111   (Other):1372   (Other):2411

Πριν προχωρήσουμε, θα κάνουμε έναν έλεγχο για τυχόν διπλότυπα. Ακολουθούμε τις συμβουλές του geeksforgeeks για να εντοπίσουμε το πλήθος των διπλοτύπων:

# Πόσα διπλότυπα;
sum(duplicated(sampled_mushrooms))
[1] 28

Βλέπουμε ότι έχουμε 28 διπλότυπα. Τα εξοστρακίζουμε ως ακολούθως:

# Απόρριψη διπλοτύπων
sampled_mushrooms <- unique(sampled_mushrooms)

Ελέγχουμε επίσης για ελλειπούσες τιμές (ΝΑ).

sum(is.na(sampled_mushrooms))
[1] 0

Έχουμε 0 ελλειπούσες τιμές, άρα το επόμενο βήμα δεν προσφέρει απολύτως τύποτα. Το παραθέτουμε απλώς στα πλαίσια μιας γενικότερης προσέγγισης.

sampled_mushrooms <- sampled_mushrooms[complete.cases(sampled_mushrooms),]

Κι ας ρίξουμε μια ματιά στο νέο μας dataframe.

# Dataframe χωρίς διπλότυπα;
str(sampled_mushrooms)
'data.frame':   14972 obs. of  10 variables:
 $ class     : Factor w/ 2 levels "e","p": 2 2 1 2 1 2 2 1 1 2 ...
 $ Feature_7 : num  25.02 26.7 3.14 12.79 20.14 ...
 $ Feature_11: Factor w/ 4 levels "a","s","u","w": 3 1 1 1 3 1 1 2 1 3 ...
 $ Feature_6 : num  14.69 6.68 4.92 4.35 27.41 ...
 $ Feature_2 : Factor w/ 7 levels "b","c","f","o",..: 7 3 1 7 3 7 1 4 6 1 ...
 $ Feature_10: Factor w/ 8 levels "d","g","h","l",..: 1 1 2 1 1 1 2 1 4 5 ...
 $ Feature_8 : Factor w/ 13 levels "b","e","f","g",..: 13 12 13 12 7 2 7 5 12 7 ...
 $ Feature_1 : num  12.49 18.91 3.04 5.11 18.98 ...
 $ Feature_5 : Factor w/ 12 levels "b","e","f","g",..: 7 11 11 11 11 2 6 12 11 4 ...
 $ Feature_4 : logi  FALSE TRUE FALSE TRUE FALSE FALSE ...

Βλέπουμε ότι πλέον έχουμε 14972 τιμές για κάθε μεταβλητή, αντί των αρχικών 15000. Όπερ σημαίνει ότι αφαιρέθηκαν τα διπλότυπα που εντοπίσαμε.

Κλείνοντας με τη συνολική προεπεξεργασία των δεδομένων μας, ας ρίξουμε μια νέα ματιά εν συνόλω μέσω ενός grid-plot. Προς τούτο θα χρησιμοποιήσουμε τη συνάρτηση ggpairs() του πακέτου GGally ακολουθώντας τις οδηγίες από εδώ. Κατόπιν υποδίξεως του διδάσκοντος δεν θα απεικονίσουμε όλα τα δεδομένα του sampled_mushrooms, αλλά 1000 τυχαίες γραμμές του εν λόγω dataframe:

# Η βάση της τυχαιότητας ορίζεται ίδια με πριν
set.seed(student_id)

# Ορίζουμε μια λίστα 1000 τυχαίων αριθμών από το σύνολο {1, 2, 3, 4,...,15000}
sampleR <- sample(nrow(sampled_mushrooms), size = 1000, replace=F)

# Φτιάχνουμε το grid-plot από 1000 τυχαίες γραμμές του sampled_mushrooms
ggpairs(sampled_mushrooms[sampleR,])
`stat_bin()` using `bins = 30`. Pick better value `binwidth`.
`stat_bin()` using `bins = 30`. Pick better value `binwidth`.
`stat_bin()` using `bins = 30`. Pick better value `binwidth`.
`stat_bin()` using `bins = 30`. Pick better value `binwidth`.
`stat_bin()` using `bins = 30`. Pick better value `binwidth`.
`stat_bin()` using `bins = 30`. Pick better value `binwidth`.
`stat_bin()` using `bins = 30`. Pick better value `binwidth`.
`stat_bin()` using `bins = 30`. Pick better value `binwidth`.
`stat_bin()` using `bins = 30`. Pick better value `binwidth`.
`stat_bin()` using `bins = 30`. Pick better value `binwidth`.
`stat_bin()` using `bins = 30`. Pick better value `binwidth`.
`stat_bin()` using `bins = 30`. Pick better value `binwidth`.
`stat_bin()` using `bins = 30`. Pick better value `binwidth`.
`stat_bin()` using `bins = 30`. Pick better value `binwidth`.
`stat_bin()` using `bins = 30`. Pick better value `binwidth`.
`stat_bin()` using `bins = 30`. Pick better value `binwidth`.
`stat_bin()` using `bins = 30`. Pick better value `binwidth`.
`stat_bin()` using `bins = 30`. Pick better value `binwidth`.
`stat_bin()` using `bins = 30`. Pick better value `binwidth`.
`stat_bin()` using `bins = 30`. Pick better value `binwidth`.
`stat_bin()` using `bins = 30`. Pick better value `binwidth`.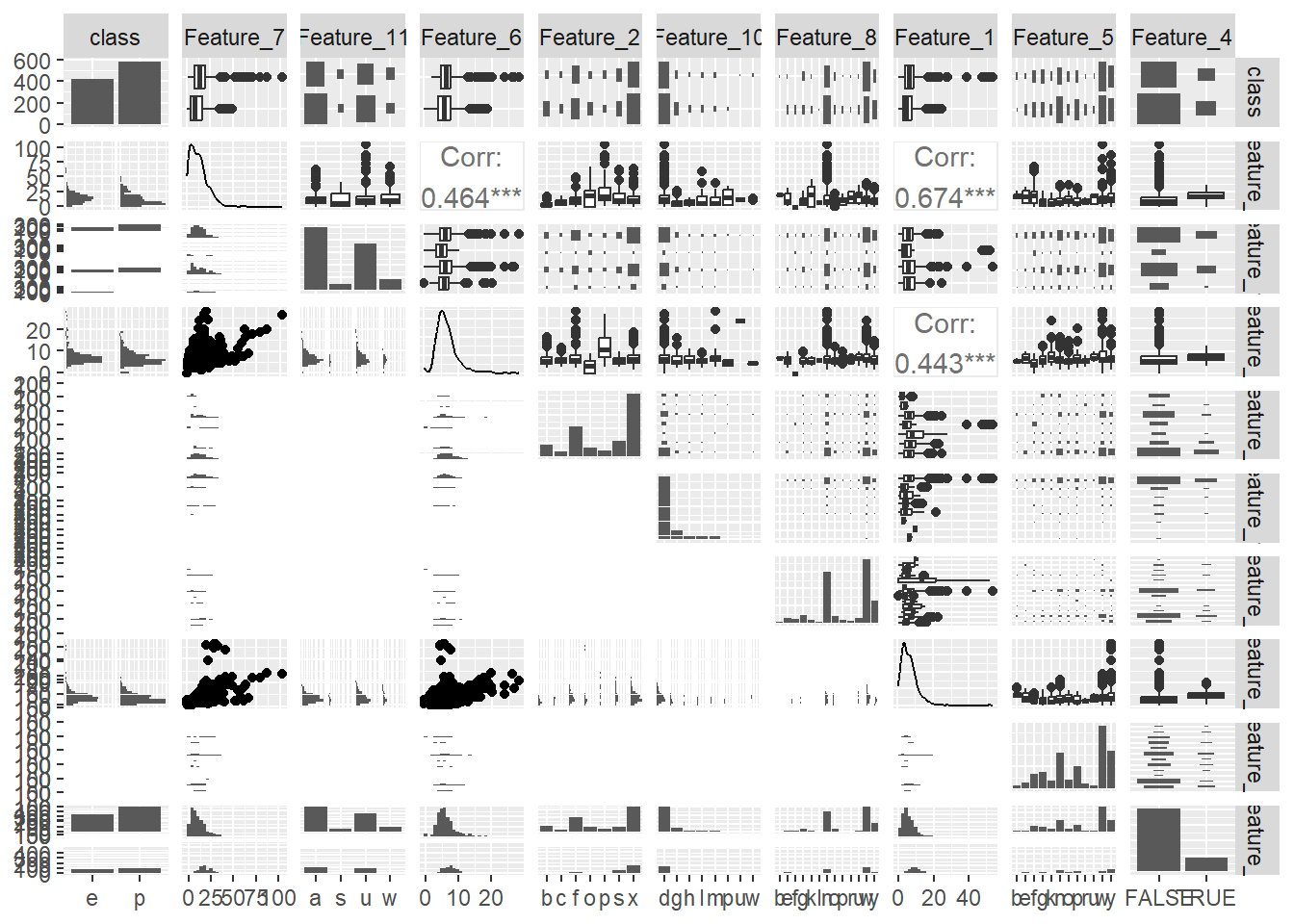

4 Δέντρα αποφάσεων

4.1 Απλή μοντελοποίηση - όλα τα δεδομένα

Στην ενότητα αυτή θα ακολουθήσουμε τις οδηγίες του Introduction to Machine Learning with R. Έτσι, αρχικά υπολογίζουμε το 75% των γραμμών και το στρογυλοποιούμε, διότι (προφανώς) θα πρέπει να είναι ακέραιος, κάθόσον ακολούθως θα επιλέξουμε το 75% των γραμμών.

# Η βάση της τυχαιότητας ορίζεται ίδια με πριν
set.seed(student_id)

# Υπολογίζουμε το 75% των γραμμών
sample_size <- floor(0.75 * nrow(sampled_mushrooms))
# Επιλέγουμε τυχαία τους δείκτες των γραμμών που θα χρησιμοποιήσουμε για εκπαίδευση
train_index <- sample(nrow(sampled_mushrooms), size = sample_size, replace=F)

Κατόπιν ορίζουμε το σύνολο εκπαίδευσης (75% των γραμμών) και το σύνολο ελέγχου (τα υπόλοιπα).

# Δημιουργία των συνόλων εκπαίδευσης κι ελέγχου
train_set <- sampled_mushrooms[train_index, ]
test_set <- sampled_mushrooms[-train_index, ]

Το δέντρο μας είναι έτοιμο να φτιαχτεί. Καθόσον θέλουμε να προβλέπουμε τη μεταβλητή class χρησιμοποιώντας όλες τις υπόλοιπες στήλες, γράφουμε class ~ ., σε αντίθεση με τις μετέπειτα προσεγγίσεις που θα γράφουμε π.χ. class ~ Feature_7 + Feature_11, εξετάζοντας έτσι την class μόνο βάσει των Feature_7 και Feature_11.

# Δημιουργία του δέντρου
tree_full <- rpart(class ~ ., 
                   data = train_set, 
                   method = "class" # Για συνεχείς μεταβλητές "anova" ΝΑ ΔΩ!!!
                   )
# Οπτικοποίηση με το rpart.plot, καθόσον βγαίνει ευκρινέστερο από το plot
rpart.plot(tree_full, main = "Δέντρο Απόφασης (Όλα τα χαρακτηριστικά)")

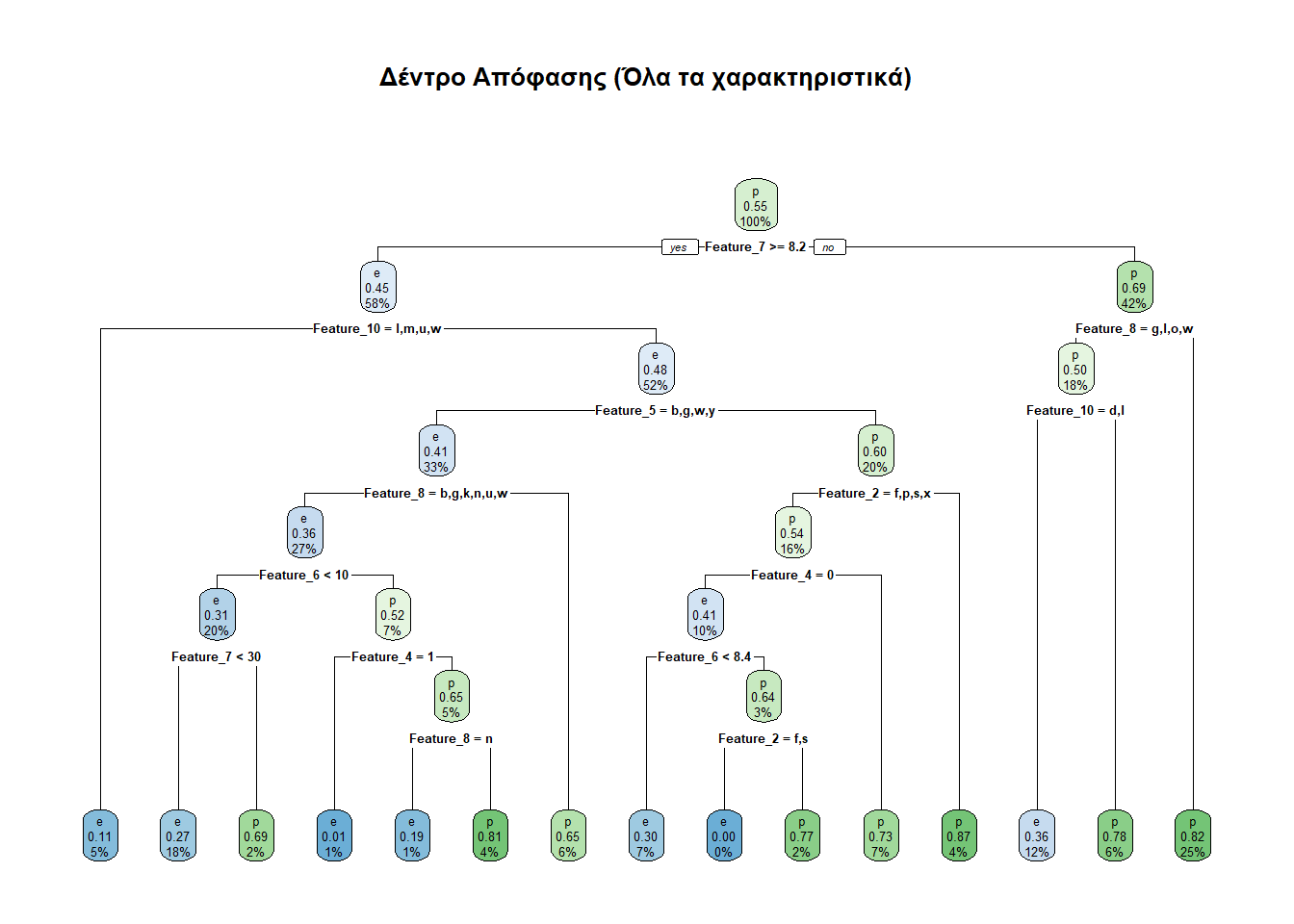
Ας εξετάσουμε τώρα πόσο καλές προβλέψεις δίνει το μοντέλο μας.

prediction <- predict(tree_full, test_set, type = "class")
(predictionTable <- table(prediction, test_set$class))
          
prediction    e    p
         e 1196  489
         p  404 1654

Αναλυτικότερα, ο πίνακας αυτός λέει τα παρακάτω:

  • Διαπιστώθηκαν ορθώς ως εδώδιμα (e) 1196 μανιτάρια.

  • Διαπιστώθηκαν εσφαλμένα ως εδώδιμα (e) 489 μανιτάρια.

  • Διαπιστώθηκαν ορθώς ως δηλητηριώδη (p) 1654 μανιτάρια.

  • Διαπιστώθηκαν εσφαλμένα ως δηλητηριώδη (p) 404 μανιτάρια.

4.2 Απλή μοντελοποίηση - Feature_7 και Feature_11

Ας πάμε τώρα να φτιάξουμε δέντρα χρησιμοποιώντας μέρος των διαθέσιμων χαρακτηριστικών. Σε πρώτη φάση θα λάβουμε υπ’ όψιν μόνο τα Feature_7 και Feature_11.

# Μοντέλο 2: Χρήση μόνο των Feature_7 και Feature_11
tree_part1 <- rpart(class ~ Feature_7 + Feature_11, 
                    data = train_set, 
                    method = "class")
rpart.plot(tree_part1, main = "Δέντρο Απόφασης (Χαρακτηριστικά Feature_7 και Feature_11)")

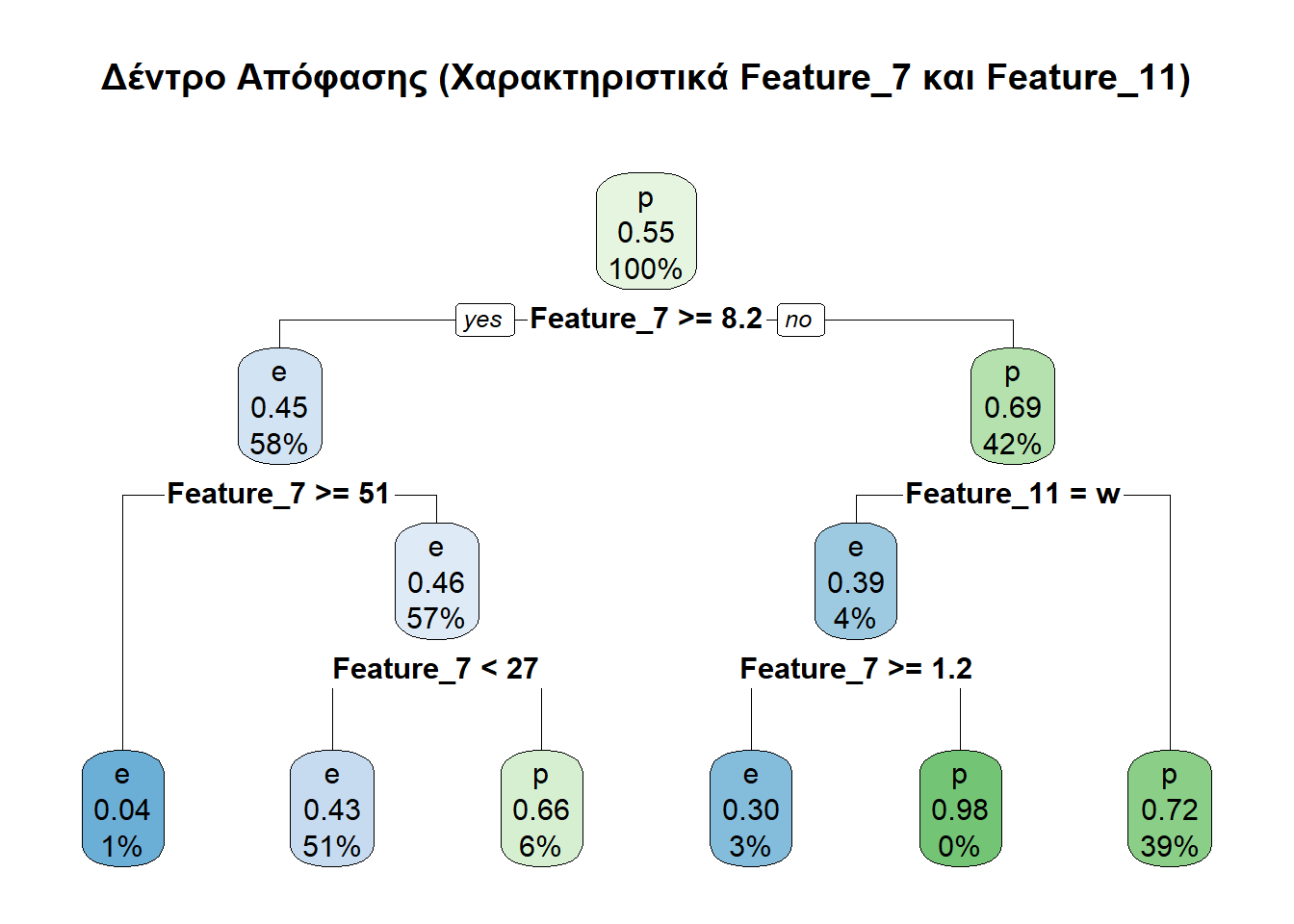
Ας εξετάσουμε και τις αντίστοιχες προβλέψεις.

prediction1 <- predict(tree_part1, test_set, type = "class")
(predictionTable1 <- table(prediction1, test_set$class))
           
prediction1    e    p
          e 1127  922
          p  473 1221

Ο παραπάνω πίνακας λέει τα κάτωθι:

  • Διαπιστώθηκαν ορθώς ως εδώδιμα (e) 1127 μανιτάρια.

  • Διαπιστώθηκαν εσφαλμένα ως εδώδιμα (e) 922 μανιτάρια.

  • Διαπιστώθηκαν ορθώς ως δηλητηριώδη (p) 1221 μανιτάρια.

  • Διαπιστώθηκαν εσφαλμένα ως δηλητηριώδη (p) 473 μανιτάρια.

4.3 Απλή μοντελοποίηση - Feature_6, Feature_2 και Feature_4

Ας κάνουμε κι ένα άλλο δέντρο βασισμένο σε άλλα χαρακτηριστικά, συγκεκριμένα τα Feature_6, Feature_2 και Feature_4.

# Μοντέλο 3: Χρήση των Feature_6, Feature_2 και Feature_4
tree_part2 <- rpart(class ~ Feature_6 + Feature_2 + Feature_4, 
                    data = train_set, 
                    method = "class")
rpart.plot(tree_part2, main = "Δέντρο Απόφασης (Χαρακτηριστικά Feature_6 + Feature_2 + Feature_4)")

prediction2 <- predict(tree_part2, test_set, type = "class")
(predictionTable2 <- table(prediction2, test_set$class))
           
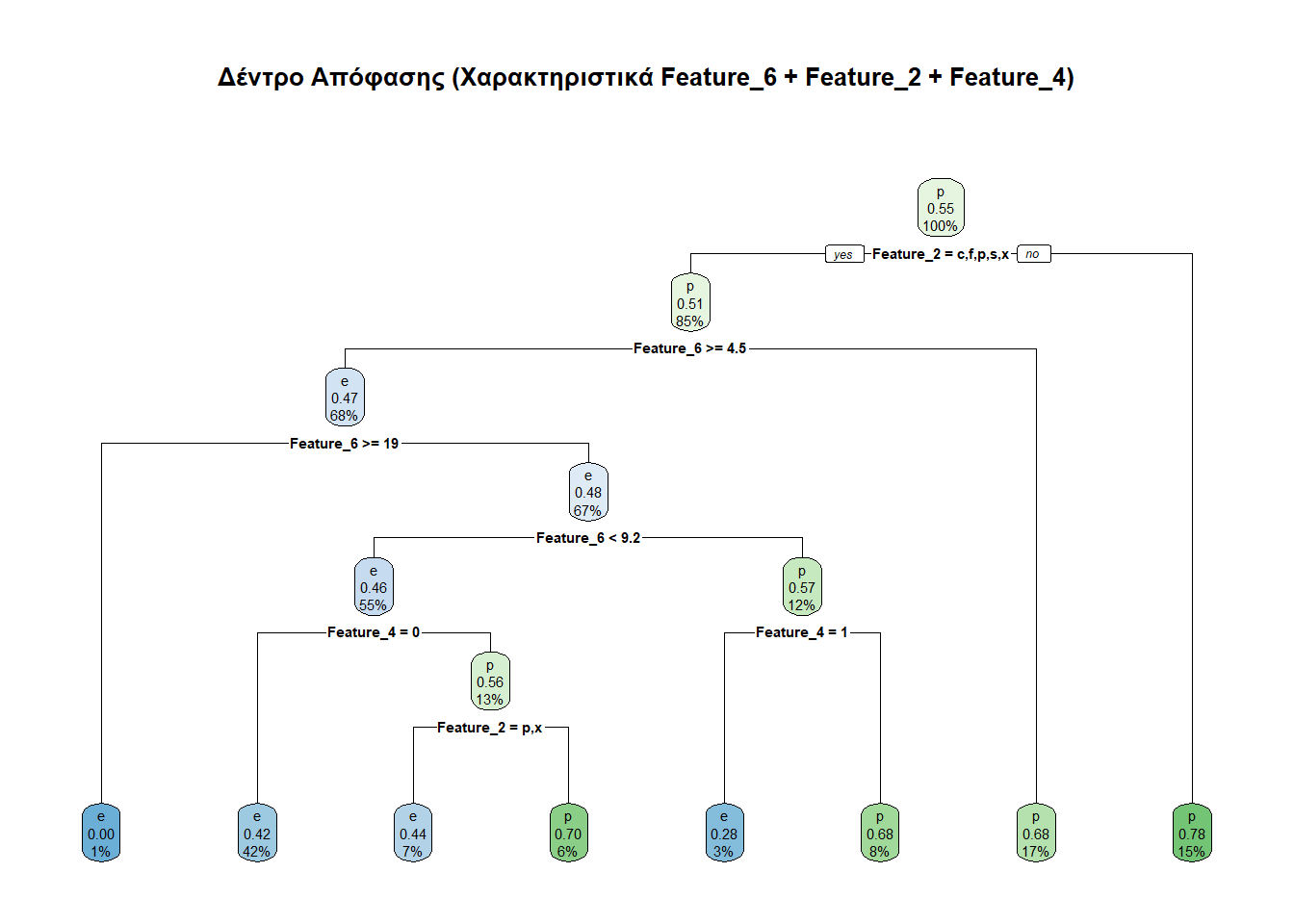
prediction2    e    p
          e 1101  871
          p  499 1272

Ο παραπάνω πίνακας λέει τα κάτωθι:

  • Διαπιστώθηκαν ορθώς ως εδώδιμα (e) 1101 μανιτάρια.

  • Διαπιστώθηκαν εσφαλμένα ως εδώδιμα (e) 871 μανιτάρια.

  • Διαπιστώθηκαν ορθώς ως δηλητηριώδη (p) 1272 μανιτάρια.

  • Διαπιστώθηκαν εσφαλμένα ως δηλητηριώδη (p) 499 μανιτάρια.

4.4 Με initial_split

Στην υποενότητα αυτή θα ακολουθήσουμε μια πιο αυτοματοποιημένη, αλλά και πιο στατιστικά αμερόληπτη μέθοδο. Συγκεκριμένα, προκειμένου να καταλήγουμε σε αντιπροσωπευτικό δείγμα (όχι bias), θα πρέπει οι αναλογίες των τιμών της class να είναι παρόμοιες σε κάθε δείγμα που θα διαλέξουμε. Προς τούτο θα ακολουθήσουμε τις οδηγίες του Practical Machine Learning with R και θα χρησιμοποιήσουμε τη συνάρτηση initial_split() του πακέτου tidymodels.

# Η βάση της τυχαιότητας ορίζεται ίδια με πριν
set.seed(student_id)

# Το prop έχει προεπιλογή το 0.75
Split7525 = initial_split(sampled_mushrooms, prop = 0.75, strata = class)

# Εξαγωγή των συνόλων:
trainIS = training(Split7525)
testIS  = testing(Split7525)
# Μοντέλο initial_split
treeIS <- rpart(class ~ ., 
                    data = trainIS, 
                    method = "class")
rpart.plot(treeIS, main = "Δέντρο Απόφασης (Όλα τα χαρακτηριστικά - με initial_split)")

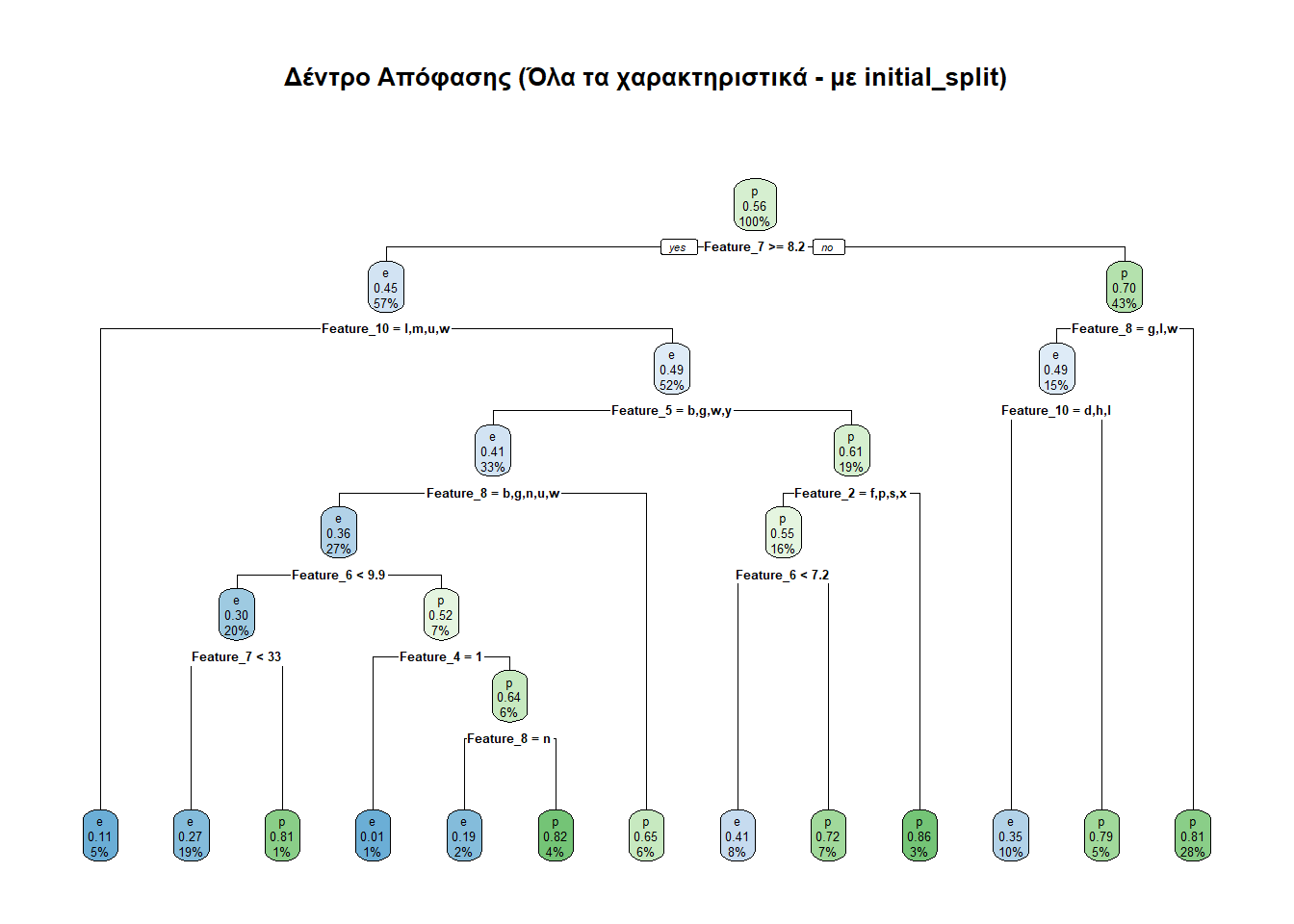
Ας δούμε και τις προβλέψεις που κάνει αυτό το μοντέλο.

predictionIS <- predict(treeIS, testIS, type = "class")
(predictionTableIS <- table(predictionIS, testIS$class))
            
predictionIS    e    p
           e 1172  537
           p  487 1548

Ο παραπάνω πίνακας λέει τα κάτωθι:

  • Διαπιστώθηκαν ορθώς ως εδώδιμα (e) 1172 μανιτάρια.

  • Διαπιστώθηκαν εσφαλμένα ως εδώδιμα (e) 537 μανιτάρια.

  • Διαπιστώθηκαν ορθώς ως δηλητηριώδη (p) 1548 μανιτάρια.

  • Διαπιστώθηκαν εσφαλμένα ως δηλητηριώδη (p) 487 μανιτάρια.

4.5 Με createDataPartition

Στα ίδια πλαίσια είναι και η συνάρτηση createDataPartition() του πακέτου caret. Ο γράφων βρήκε αυτή την προσέγγιση εδώ. Η άποψη LLM που ρώτησε (DeepSeek, Gemini και ChatGPT) είναι ότι η συνάρτηση createDataPartition() του πακέτου caret κάνει την ίδια δουλειά με τη συνάρτηση initial_split() του πακέτου tidymodels, την οποία χρησιμοποιήσαμε σε προηγούμενη ενότητα. Παραταύτα, για λόγους επαλήθευσης των λεγομένων τους, αλλά και μετέπειτα αξιοποίησης του πακέτου caret ο γράφων προχώρησε και στη μελέτη με την createDataPartition().

# Η βάση της τυχαιότητας ορίζεται ίδια με πριν
set.seed(student_id)

# Διατηρεί την αναλογία της μεταβλητής 'class'
train_index_caret <- createDataPartition(
  sampled_mushrooms$class,
  p = 0.75,
  list = FALSE # Για να μου βγάλει vector
  )

trainCaret <- sampled_mushrooms[train_index_caret, ]
testCaret  <- sampled_mushrooms[-train_index_caret, ]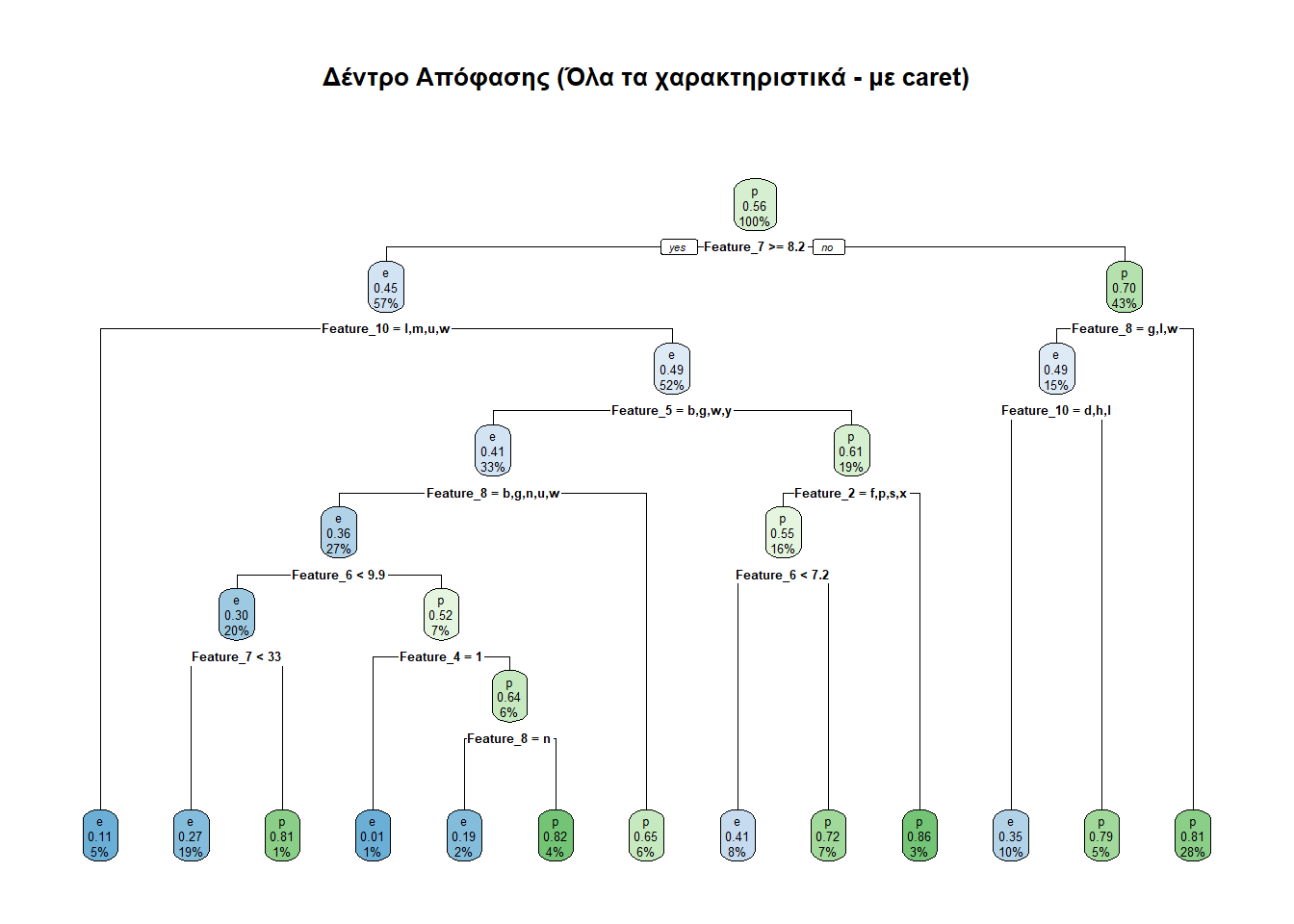
# Μοντέλο caret
treeCaret <- rpart(class ~ ., data = trainCaret, method = "class")
rpart.plot(treeCaret, main = "Δέντρο Απόφασης (Όλα τα χαρακτηριστικά - με caret)")

Ας δούμε και τις προβλέψεις που κάνει αυτό το μοντέλο.

predictionC <- predict(treeCaret, testCaret, type = "class")
(predictionTableC <- table(predictionC, testCaret$class))
           
predictionC    e    p
          e 1171  537
          p  487 1547

Ο παραπάνω πίνακας λέει τα κάτωθι:

  • Διαπιστώθηκαν ορθώς ως εδώδιμα (e) 1171 μανιτάρια.

  • Διαπιστώθηκαν εσφαλμένα ως εδώδιμα (e) 537 μανιτάρια.

  • Διαπιστώθηκαν ορθώς ως δηλητηριώδη (p) 1547 μανιτάρια.

  • Διαπιστώθηκαν εσφαλμένα ως δηλητηριώδη (p) 487 μανιτάρια.

# Συνάρτηση που επιστρέφει το Accuracy από το αντικείμενο της caret
evaluate_model_caret <- function(model, test_set) {
  pred <- predict(model, test_set, type = "class")
  # Το confusionMatrix θέλει τα levels να είναι factors
  cm <- confusionMatrix(data = pred, reference = as.factor(test_set$class))
  return(cm$overall['Accuracy'])
}

# Εκτύπωση αποτελεσμάτων
print(paste("Full Model Accuracy:", evaluate_model_caret(tree_full_c, test_data_c)))
print(paste("Subset 1 Accuracy:", evaluate_model_caret(tree_sub1_c, test_data_c)))
print(paste("Subset 2 Accuracy:", evaluate_model_caret(tree_sub2_c, test_data_c)))

# Αν θέλεις να δεις ΟΛΑ τα στατιστικά για το πρώτο μοντέλο:
pred_full <- predict(tree_full_c, test_data_c, type = "class")
confusionMatrix(pred_full, as.factor(test_data_c$class))

4.6 Αξιολόγηση δέντρων

Πριν προχωρήσουμε στην αξιολόγηση των δέντρων που δημιουργήσαμε, αναφέρουμε τις έννοιες βάσει των οποίων θα αξιολογηθούν:

  • Ακρίβεια (accuracy) είναι το ποσοστό των εύστοχων απαντήσεων, δηλαδή το ποσοστό των απαντήσεων που τα μανητάρια ανιχνεύτηκαν ορθώς ως εδώδιμα ή δηλητηριώδη.

    1. Μαθηματικά μιλώντας, είναι η ποσότητα:

    \[ \dfrac{[TruePoisonous]+[TrueEdible]}{[TruePoisonous]+[TrueEdible]+[FalsePoisonous]+[FalseEdible]} \]

    1. Προγραμματιστικά μιλώντας είναι η συνάρτηση:
accuracyFunc <- function(myTable){
  (myTable[1,1]+myTable[2,2])/(myTable[1,1]+myTable[2,2]+myTable[1,2]+myTable[2,1])
}

  • Ευστοχία (precision) είναι το ποσοστό των ορθών απαντήσεων από τις γνωματεύσεις «Είναι εδώδιμο».

    1. Μαθηματικά μιλώντας, είναι η ποσότητα:

    \[ \dfrac{[TrueEdible]}{[TrueEdible]+[FalseEdible]} \]

    1. Προγραμματιστικά μιλώντας είναι η συνάρτηση:
precisionFunc <- function(myTable){
  (myTable[1,1])/(myTable[1,1]+myTable[1,2])
}

  • Ανάκληση ή ευαισθησία (recall ή sensitivity) είναι το ποσοστό των εύστοχων απαντήσεων που δίνονται όταν εξετάζονται εδώδιμα μανιτάρια.

    1. Μαθηματικά μιλώντας, είναι η ποσότητα:

    \[ \dfrac{[TrueEdible]}{[TrueEdible]+[FalsePoisonous]} \]

    1. Προγραμματιστικά μιλώντας είναι η συνάρτηση:
recallFunc <- function(myTable){
  (myTable[1,1])/(myTable[1,1]+myTable[2,1])
}

  • Ειδικότητα (specificity) είναι το ποσοστό των εύστοχων απαντήσεων που δίνονται όταν εξετάζονται δηλητιριώδη μανιτάρια.

    1. Μαθηματικά μιλώντας, είναι η ποσότητα:

    \[ \dfrac{[TruePoisonous]}{[TruePoisonous]+[FalseEdible]} \]

    1. Προγραμματιστικά μιλώντας είναι η συνάρτηση:
specificityFunc <- function(myTable){
  (myTable[2,2])/(myTable[2,2]+myTable[1,2])
}

Θα παρουσιάσουμε την αξιολόγηση των δέντρων που φτιάξαμε με έναν πίνακα.

SampleTree.AllFeatures <- c(accuracyFunc(predictionTable),precisionFunc(predictionTable),recallFunc(predictionTable),specificityFunc(predictionTable))

SampleTree.Features7.11 <- c(accuracyFunc(predictionTable1),precisionFunc(predictionTable1),recallFunc(predictionTable1),specificityFunc(predictionTable1))

SampleTree.Features2.4.6 <- c(accuracyFunc(predictionTable2),precisionFunc(predictionTable2),recallFunc(predictionTable2),specificityFunc(predictionTable2))

InitialSplitTree.AllFeatures <- c(accuracyFunc(predictionTableIS),precisionFunc(predictionTableIS),recallFunc(predictionTableIS),specificityFunc(predictionTableIS))

CaretSplitTree.AllFeatures <- c(accuracyFunc(predictionTableC),precisionFunc(predictionTableC),recallFunc(predictionTableC),specificityFunc(predictionTableC))

resultsDF <- data.frame(SampleTree.AllFeatures, SampleTree.Features7.11, SampleTree.Features2.4.6, InitialSplitTree.AllFeatures, CaretSplitTree.AllFeatures)

rownames(resultsDF) <- c("accuracy", "precision", "recall", "specificity")
knitr::kable(head(resultsDF)) %>%
  kable_styling("striped", full_width = T) %>%
  scroll_box(width = "100%", height = "max-content")
SampleTree.AllFeatures SampleTree.Features7.11 SampleTree.Features2.4.6 InitialSplitTree.AllFeatures CaretSplitTree.AllFeatures
accuracy 0.7614213 0.6273043 0.6339834 0.7264957 0.7263495
precision 0.7097923 0.5500244 0.5583164 0.6857812 0.6855972
recall 0.7475000 0.7043750 0.6881250 0.7064497 0.7062726
specificity 0.7718152 0.5697620 0.5935604 0.7424460 0.7423225

Βλέπουμε ότι το να εξετάσουμε όλα τα χαρακτηριστικά των μανηταριών δίνει καλύτερα μέτρα επίδοσης, όπερ αναμενόμενον. Επίσης οι συναρτήσεις initial_split() και createDataPartition() παρήγαγαν παρόμοιας αξιοπιστίας αποτελέσματα, όπως είχαμε ενημερωθεί από διάφορα LLM. Αυτό το οποίο δεν ήταν αναμενόμενο είναι η εμφανής υστέρηση των αποτελεσμάτων που έκαναν χρήση των συναρτήσεων initial_split() και createDataPartition(), έναντι της απλής δειγματοληψίας (sample).

Τα εν λόγω αποτελέσματα προκάλεσαν έκπληξη στον γράφοντα. Μία σκέψη ήταν ότι οι εν λόγω συναρτήσεις δεν σού αυξάνουν την ακρίβεια της γενίκευσης, αλλά την βεβαιότητα ότι η γενίκευση που επιτυγχάνει το μοντέλο θα έχει όντως αυτή την ακρίβεια. Από την άλλη η τοποθέτηση LLM (DeepSeek) επί του ζητήματος ήταν:

Παρόλο που το stratified sampling θεωρητικά είναι καλύτερο, μπορεί να έχει προβλήματα όταν:

  • Οι κλάσεις είναι ήδη ισορροπημένες (όπως φαίνεται στα δεδομένα σου).

  • Η διαστρωμάτωση δημιουργεί πιο «δύσκολα» test sets.

  • Το δέντρο δεν μπορεί να γενικεύσει καλά στα stratified splits.

Στα πλαίσια αυτά επιχειρήθηκε αναλυτικότερη μελέτη χρησιμοποιώντας τη συνάρτηση confusionMatrix() του πακέτου caret.

confusionMatrix(prediction, as.factor(test_set$class))
Confusion Matrix and Statistics

          Reference
Prediction    e    p
         e 1196  489
         p  404 1654
                                         
               Accuracy : 0.7614         
                 95% CI : (0.7474, 0.775)
    No Information Rate : 0.5725         
    P-Value [Acc > NIR] : < 2e-16        
                                         
                  Kappa : 0.5158         
                                         
 Mcnemar's Test P-Value : 0.00494        
                                         
            Sensitivity : 0.7475         
            Specificity : 0.7718         
         Pos Pred Value : 0.7098         
         Neg Pred Value : 0.8037         
             Prevalence : 0.4275         
         Detection Rate : 0.3195         
   Detection Prevalence : 0.4502         
      Balanced Accuracy : 0.7597         
                                         
       'Positive' Class : e              
                                         
confusionMatrix(prediction1, as.factor(test_set$class))
Confusion Matrix and Statistics

          Reference
Prediction    e    p
         e 1127  922
         p  473 1221
                                          
               Accuracy : 0.6273          
                 95% CI : (0.6116, 0.6428)
    No Information Rate : 0.5725          
    P-Value [Acc > NIR] : 5.238e-12       
                                          
                  Kappa : 0.2647          
                                          
 Mcnemar's Test P-Value : < 2.2e-16       
                                          
            Sensitivity : 0.7044          
            Specificity : 0.5698          
         Pos Pred Value : 0.5500          
         Neg Pred Value : 0.7208          
             Prevalence : 0.4275          
         Detection Rate : 0.3011          
   Detection Prevalence : 0.5474          
      Balanced Accuracy : 0.6371          
                                          
       'Positive' Class : e               
                                          
confusionMatrix(prediction2, as.factor(test_set$class))
Confusion Matrix and Statistics

          Reference
Prediction    e    p
         e 1101  871
         p  499 1272
                                          
               Accuracy : 0.634           
                 95% CI : (0.6183, 0.6494)
    No Information Rate : 0.5725          
    P-Value [Acc > NIR] : 1.099e-14       
                                          
                  Kappa : 0.2736          
                                          
 Mcnemar's Test P-Value : < 2.2e-16       
                                          
            Sensitivity : 0.6881          
            Specificity : 0.5936          
         Pos Pred Value : 0.5583          
         Neg Pred Value : 0.7182          
             Prevalence : 0.4275          
         Detection Rate : 0.2941          
   Detection Prevalence : 0.5269          
      Balanced Accuracy : 0.6408          
                                          
       'Positive' Class : e               
                                          
confusionMatrix(predictionIS, as.factor(testIS$class))
Confusion Matrix and Statistics

          Reference
Prediction    e    p
         e 1172  537
         p  487 1548
                                          
               Accuracy : 0.7265          
                 95% CI : (0.7119, 0.7407)
    No Information Rate : 0.5569          
    P-Value [Acc > NIR] : <2e-16          
                                          
                  Kappa : 0.4475          
                                          
 Mcnemar's Test P-Value : 0.1257          
                                          
            Sensitivity : 0.7064          
            Specificity : 0.7424          
         Pos Pred Value : 0.6858          
         Neg Pred Value : 0.7607          
             Prevalence : 0.4431          
         Detection Rate : 0.3130          
   Detection Prevalence : 0.4565          
      Balanced Accuracy : 0.7244          
                                          
       'Positive' Class : e               
                                          
confusionMatrix(predictionC, as.factor(testCaret$class))
Confusion Matrix and Statistics

          Reference
Prediction    e    p
         e 1171  537
         p  487 1547
                                          
               Accuracy : 0.7263          
                 95% CI : (0.7118, 0.7406)
    No Information Rate : 0.5569          
    P-Value [Acc > NIR] : <2e-16          
                                          
                  Kappa : 0.4472          
                                          
 Mcnemar's Test P-Value : 0.1257          
                                          
            Sensitivity : 0.7063          
            Specificity : 0.7423          
         Pos Pred Value : 0.6856          
         Neg Pred Value : 0.7606          
             Prevalence : 0.4431          
         Detection Rate : 0.3129          
   Detection Prevalence : 0.4564          
      Balanced Accuracy : 0.7243          
                                          
       'Positive' Class : e

Εξετάζοντας το Mcnemar’s Test P-Value βλέπουμε ότι τα δέντρα που χρησιμοποίησαν τις συναρτήσεις initial_split() και createDataPartition() ναι μεν υστερούν σε αξιοπιστία, αλλά δίνουν πιο ισορροπημένα αποτελέσματα σε σχέση με τη μέθοδο της απλής δειγματοληψίας (αυτή ειχε p-τιμή αρκετά μικρότερη του 0.05). Δηλαδή δεν ευνοούν τα λάθη τύπου «διάγνωση δηλητηριώδους ως εδώδιμου» έναντι λαθών τύπου «διάγνωση εδώδιμου ως δηλητηριώδους». Και σε αυτό το σημείο τελειώνει η μελέτη αυτής της ενότητας.

5 Random forest

5.1 Με το χέρι

Σύμφωνα με την εργασία ο αριθμός των δέντρων έπρεπε να είναι \(1000\). Αυτό, όμως, έκανε τον υπολογιστή του γράφοντος να κολλήσει, επομένως ήταν αναπόδραστο το να μειωθεί ο αριθμός τους σε \(10\). Ο γράφων επιφυλάσσεται για τη μελέτη 1000 δέντρων στην επόμενη ενότητα, που θα γίνει το τυχαίο δάσος με έτοιμη συνάρτηση της R.

n_trees <- 10

Αρχινάμε τη δημιουργία του δάσους.

set.seed(student_id)

forest_models <- replicate(n_trees, {
  # Δημιουργία bootstrap δείγματος
  bootstrap_sample <- train_set[sample(nrow(train_set), replace = TRUE), ]
  
  # Εκπαίδευση και επιστροφή του δέντρου
  rpart(class ~ ., data = bootstrap_sample, method = "class", 
        control = rpart.control(minsplit = 2, cp = 0.01))
}, 
simplify = FALSE
)

Ας δούμε τώρα τι προβλέψεις κάνει το κάθε μοντέλο.

all_preds <- sapply(forest_models,# τα δέντρα που φτιάξαμε
                    predict,# εφαρμόζουμε την predict σε κάθε ένα τους
                    newdata = test_set, type = "class" # οι παράμετροι της predict
                    )

Ακολούθως ψάχνουμε να βρούμε τις πιο διαδεδομένες προβλέψεις των δέντρων για κάθε περίπτωση.

final_predictions <- apply(all_preds, # οι προβλέψεις μας
                           1, # εφαρμογή της παρακάτω συνάρτησης σε κάθε γραμμή (2 για στήλες)
                           function(x) names(which.max(table(x))) # Εύρεση της πρόβλεψης (names) με τη μέγιστη (which.max) συχνότητα (table)
                           )

final_predictions <- factor(final_predictions, levels = levels(test_set$class))

Τώρα μπορούμε να φτιάξουμε έναν πίνακα με τις προβλέψεις μας.

(rf_conf_matrix <- table(Πρόβλεψη = final_predictions, Πραγματικό = test_set$class))
        Πραγματικό
Πρόβλεψη    e    p
       e 1273  498
       p  327 1645

Σύμφωνα με τον πίνακα αυτόν η ακρίβεια είναι 0.7795886. Το γεγονός ότι είναι τόσο μικρή οφείλεται στον μκρό αριθμό δέντρων, απόρροια των δυνατοτήτων του υπολογιστή του γράφοντος. Για ακριβέστερες προβλέψεις χρησιμοποιώντας περισσότερα δέντρα θα αξιοποιήσουμε πακέτα της R που κάνουν πρακτικά τη δουλειά με C++, άρα πολύ γρηγορότερα.

5.2 Αυτόματο

Για την αυτοματοποιημένη διαδικασία του τυχαίου δάσους, μπορούμε να απευθυνθούμε στα πακέτα randomForest και ranger. Σύμφωνα με αυτή την ανάλυση και αυτή την εργασία το ranger είναι προτιμότερο.

Σε πρώτη φάση εκπαιδεύουμε το μοντέλο μας.

set.seed(student_id)

rf_model <- ranger(
  formula = class ~ ., 
  data    = train_set, 
  num.trees = 1000, # Πλέον μπορούμε να έχουμε 1000 δέντρα
  importance = 'impurity' # Για να δούμε τη σημαντικότητα των μεταβλητών
)

Ακολούθως ας δούμε και το τι θα μπορέσει να προβλέψει. Αρχικά φτιάχνουμε τη λίστα με τις προβλέψεις επί του συνόλου ελέγχου.

rf_preds <- predict(rf_model, data = test_set)
final_predictions <- rf_preds$predictions

Ακολούθως πάμε να δούμε πόσα κατάφερε να προβλέψει σωστά και πόσα λάθος.

rf_conf_matrix <- table(Πρόβλεψη = final_predictions, Πραγματικό = test_set$class)
rf_conf_matrix
        Πραγματικό
Πρόβλεψη    e    p
       e 1564   36
       p   36 2107

Από τα παραπάνω, καταλαβαίνουμε ότι έχουμε ακρίβεια 0.9807641.

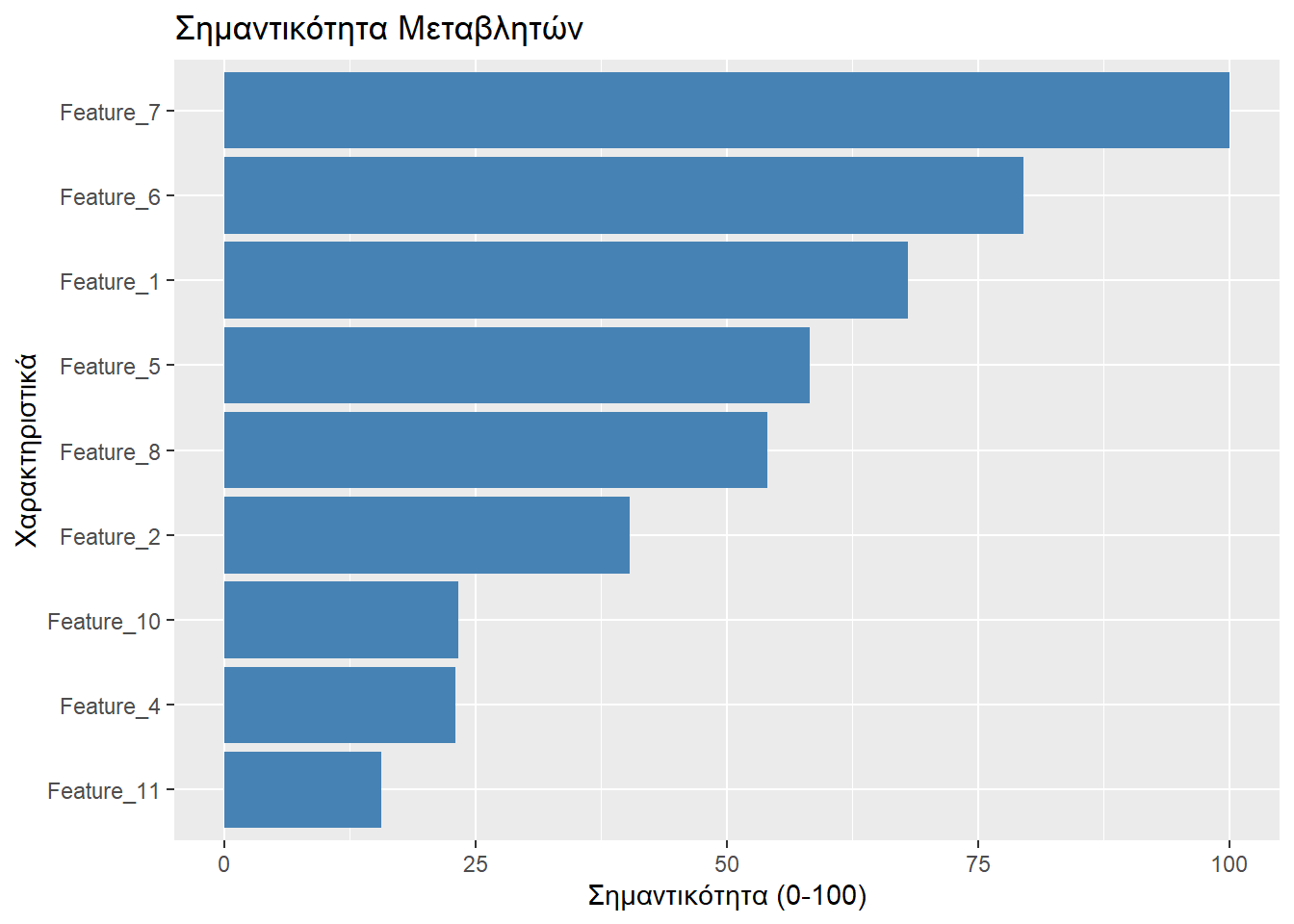
Το πακέτο ranger παρέχει τη δυνατότητα να αξιολογήσουμε τη συμβολή του κάθε χαρακτηριστικού στην ταξινόμηση των μανηταριών. Θα δώσουμε την τιμή 100 στο χαρακτηριστικό που έχει τη μέγιστη σημαντικότητα, έτσι τα υπόλοιπα θα έχουν σημαντικότητες που θα είναι ποσοστά αυτής.

imp <- importance(rf_model)
normalized_imp <- (imp / max(imp)) * 100
sort(normalized_imp, decreasing = TRUE)
 Feature_7  Feature_6  Feature_1  Feature_5  Feature_8  Feature_2 Feature_10 
 100.00000   79.48800   68.06332   58.24996   54.04559   40.37648   23.33637 
 Feature_4 Feature_11 
  23.01842   15.66153

Ας δούμε και γραφικά τα παραπάνω.

# Μετατροπή του διανύσματος σε Data Frame
imp_df <- data.frame(
  Feature = names(normalized_imp),
  Importance = as.numeric(normalized_imp)
)

# Δημιουργία του γραφήματος
ggplot(imp_df, aes(x = reorder(Feature, Importance), y = Importance)) + 
  geom_bar(stat = "identity", fill = "steelblue") +
  coord_flip() +  # Αντιστροφή αξόνων για να διαβάζονται τα ονόματα
  labs(
    title = "Σημαντικότητα Μεταβλητών",
    x = "Χαρακτηριστικά",
    y = "Σημαντικότητα (0-100)"
  )

΄

6 Πλησιέστεροι γείτονες

6.1 Προεργασία

Επειδή η μέθοδος k-NN δεν μπορεί να επεξεργαστεί μη-αριθμητικά δεδομένα, μετατρέπουμε όλες τις μεταβλητές σε αριθμητικές. Η προτινόμενη μέθοδος από διάφορα LLM που ρωτήθηκαν (Gemini και ChatGPT) είναι μέσω του συνδυασμού των συναρτήσεων dummyVars() και predict() του πακέτου caret.

Προς τούτο πρώτα απομονώνουμε τη μεταβλητή στόχου (class) και ξεχωρίζουμε τις μεταβλητές των χαρακτηριστικών (Feature_n).

y <- sampled_mushrooms$class
x <- sampled_mushrooms[, -which(names(sampled_mushrooms) == "class")]

Και τώρα ήρθε η ώρα για την «αριθμητικοποίηση» των μεταβλητών μας.

x_dummies <- dummyVars(~ ., data = x)
x_numeric <- predict(x_dummies, newdata = x)

Με αυτή την προσέγγιση κάθε κατηγορική ή λογική μεταβλητή μετατρέπεται σε ένα σύνολο διανυσμάτων. Συγκεκριμένα, αν μία κατηγορική μεταβλητή (\(X\)) παίρνει \(n\) πιθανές τιμές (\(a_1, a_2,\dots,a_n\)), τότε η \(X\) «σπάει» σε \(n\) διανύσματα (\(\vec{x_1}, \vec{x_2},\dots,\vec{x_n}\)), όπου στη \(i\)-στή συντεταγμένη του \(\vec{x_j}\) είναι το \(1\), αν η \(i\)-στή συντεταγμένη της \(X\) έχει την τιμή \(a_j\), αλλιώς είναι \(0\). Από μια διαφορετική οπτική γωνία ειδομένο, μπορούμε να πούμε ότι κάθε τιμή της \(X\) αντιπροσωπεύεται από ένα διάνυσμα βάσης (\(\vec{e_j}\)) του \(\mathbb{R}^n\).

Εν πάση περιπτώσει, προχωράμε. Ακολούθως, κανονικοποιούμε τα δεδομένα μας, ώστε να έχουν όλες οι μεταβλητές μέση τιμή \(0\) και τυπική απόκλιση \(1\).

x_scaled <- scale(x_numeric)

6.2 Με class (μέθοδος Hold-out)

Αρχικά επανενώνουμε τη μεταβλητή class με τα χαρακτηριστικά. Προς τούτο θα φτιάξουμε έναν νέο dataframe, ώστε το sampled_mushrooms να παραμείνει ως έχει.

sampled_mushroomsNEW <- as.data.frame(x_scaled)
sampled_mushroomsNEW$class <- y

Ακολούθως καθορίζουμε το δείγμα εκπαίδευσης και το βήμα ελέγχου μέσω της συνάρτησης createDataPartition().

# Η βάση της τυχαιότητας ορίζεται ίδια με πριν
set.seed(student_id)

# Δείκτες γραμμών που θα επιλεγούν για εκπαίδευση
train_index <- createDataPartition(sampled_mushroomsNEW$class, p = 0.75, list = FALSE)

# Τα features εκπαίδευσης
train_x <- x_scaled[train_index, ]
# Τα features ελέγχου
test_x  <- x_scaled[-train_index, ]

# Εκπαίδευση class
train_y <- y[train_index]
# Έλεγχος class
test_y  <- y[-train_index]

Είμαστε τώρα έτοιμοι να προχωρήσουμε στην εκτέλεση της k-NN.

knn_pred <- knn(
  train = train_x, # Τα δεδομένα που ξέρει το μοντέλο
  test = test_x, # Τα δεδομένα που πρέπει να μαντέψει
  cl = train_y, # Οι σωστές απαντήσεις για τα δεδομένα εκπαίδευσης
  k = 5 # Ο αριθμός των γειτόνων (εν προκειμένω βάζουμε 5 αυθαίρετα)
  )

Κλείνουμε την υποενότητα αυτή με μια αξιολόγηση αυτού που πετύχαμε.

(predictionK_NN.class <- table(Προβλεπόμενα = knn_pred, Πραγματικά = test_y))
            Πραγματικά
Προβλεπόμενα    e    p
           e 1582   64
           p   76 2020

Ο παραπάνω πίνακας λέει τα κάτωθι:

  • Διαπιστώθηκαν ορθώς ως εδώδιμα (e) 1582 μανιτάρια.

  • Διαπιστώθηκαν εσφαλμένα ως εδώδιμα (e) 64 μανιτάρια.

  • Διαπιστώθηκαν ορθώς ως δηλητηριώδη (p) 2020 μανιτάρια.

  • Διαπιστώθηκαν εσφαλμένα ως δηλητηριώδη (p) 76 μανιτάρια.

6.3 Με caret (μέθοδος Cross Validation)

Το πακέτο caret δίνει τη δυνατότητα να εκτελέσουμε εύκολα Διασταυρούμενη Επικύρωση (Cross-Validation). Στο άρθρο Hold-out vs. Cross-validation in Machine Learning διαπιστώνουμε πως, οποτεδήποτε είναι υπολογιστικά δυνατό (η Hold-out είναι ελαφρύτερη διαδικασία) θα πρέπει να την προτιμάμε. Στα πλαίσια αυτά ο γράφων βρήκε χρήσιμη την παρακάτω απάντηση στο Stack Exchange (μετάφραση κειμένου με Gemini):

Ήθελα απλώς να προσθέσω μερικές απλές κατευθυντήριες γραμμές που ανέφερε ο Andrew Ng στο μάθημά μας CS 229 στο Stanford σχετικά με τη διασταυρούμενη επικύρωση. Αυτές είναι οι πρακτικές που ακολουθεί ο ίδιος στη δουλειά του.

Έστω \(m\) ο αριθμός των δειγμάτων στο σύνολο δεδομένων σας:

  • Αν \(m \leq 20\), χρησιμοποιήστε τη διασταυρούμενη επικύρωση με παράλειψη ενός (Leave-one-out cross validation).

  • Αν \(20 < m \leq 100\), χρησιμοποιήστε την \(k\)-πτυχη διασταυρούμενη επικύρωση (\(k\)-fold cross validation) με ένα σχετικά μεγάλο \(k \leq m\), λαμβάνοντας υπόψη το υπολογιστικό κόστος.

  • Αν \(100 < m \leq 1.000.000\), χρησιμοποιήστε την κανονική \(k\)-πτυχη διασταυρούμενη επικύρωση (\(k=5\)). Εναλλακτικά, εάν δεν υπάρχει επαρκή υπολογιστική ισχύς και \(m > 10.000\), χρησιμοποιήστε τη μέθοδο κράτησης δεδομένων (hold-out cross validation).

  • Αν \(m \geq 1.000.000\), χρησιμοποιήστε τη μέθοδο κράτησης δεδομένων (hold-out cross validation), αλλά αν υπάρχει διαθέσιμη υπολογιστική ισχύς, μπορείτε να χρησιμοποιήσετε \(k\)-πτυχη διασταυρούμενη επικύρωση (\(k=5\)), εάν θέλετε να εξαντλήσετε κάθε περιθώριο απόδοσης από το μοντέλο σας.

Αρχικά ορίζουμε το πλαίσιο στο οποίο θα εκπαιδευτεί το μοντέλο μας. Η εκφώνηση της εργασίας απαιτούσε η Cross-Validation να γίνει με διαμοιρασμό των δεδομένων σε 5 μέρη και 5 ελέγχους (4 μέρη εκπαίδευση, 1 μέρος έλεγχος), όπερ και θα πράξουμε.

ctrl <- trainControl(
  method = "cv", # Cross-Validation.
  number = 5     # Τα 5 ίσα μέρη και οι 5 έλεγχοι. 
)

Ακολούθως φτιάχνουμε μια λίστα με τα πλήθη των γειτόνων (\(k\)) που θα λειτουργήσει η k-NN.

k <- seq(1,15,2) # Χρησιμοποιούμε περιττούς (μονζυγούς) αριθμούς για να μην έχουμε ποτέ «ισοπαλία» στην ψηφοφορία των γειτόνων.
kValues <- as.data.frame(k) # Η train() απαιτεί να είναι σε μορφή πίνακα με όνομα στήλης το k

Ας ξεκινήσουμε τώρα τη διαδικασία.

set.seed(student_id) 

model_knn <- train(
  # Αντί των (1) και (2), μπορούμε εναλλακτικά να γράψουμε το κάτωθι:
  # class ~ ., 
  # data = final_df,
  x = x_scaled,      # (1)
  y = y,             # (2)
  
  method = "knn",    # Για να εφαρμόσουμε k-NN. Για περισσότερα βλ.:
  # https://topepo.github.io/caret/train-models-by-tag.html
  
  trControl = ctrl,  # Εφαρμόζουμε το πλαίσιο εκπαίδευσης που ορίσαμε προηγουμένως
  
  tuneGrid = kValues # Τα πλήθη των γειτόνων που ορίσαμε να εξεταστούν
)

Κι ας δούμε τα αποτελέσματα:

model_knn
k-Nearest Neighbors 

14972 samples
   49 predictor
    2 classes: 'e', 'p' 

No pre-processing
Resampling: Cross-Validated (5 fold) 
Summary of sample sizes: 11977, 11978, 11977, 11978, 11978 
Resampling results across tuning parameters:

  k   Accuracy   Kappa    
   1  0.9808980  0.9612631
   3  0.9749532  0.9492062
   5  0.9678065  0.9347047
   7  0.9608605  0.9206373
   9  0.9533798  0.9054825
  11  0.9452313  0.8889981
  13  0.9374834  0.8732957
  15  0.9286672  0.8553674

Accuracy was used to select the optimal model using the largest value.
The final value used for the model was k = 1.

Βλέπουμε η ακρίβεια ακολουθεί μια φθίνουσα πορεία σε σχέση με το \(k\). Η καλύτερη επιλογή, συνεπώς, είναι να επιλέξουμε όσο το (υπολογιστικά) δυνατόν μικρότερο \(k\).

Ας διαπιστώσουμε τα παραπάνω και μ’ ένα γράφημα.

# Δημιουργούμε ένα γράφημα. 
# Στον οριζόντιο άξονα είναι το k και στον κάθετο η Ακρίβεια (Accuracy). 
# Το ψηλότερο σημείο του γραφήματος μας δείχνει τον "νικητή" (το καλύτερο k).
plot(model_knn)

7 Απλό νευρωνικό δίκτυο

7.1 Με nnet

Αρχικά καθορίζουμε το σύνολο εκπαίδευσης και το σύνολο ελέγχου.

# Όπως ανέκαθεν...
set.seed(student_id)


train_size <- floor(0.75 * nrow(sampled_mushrooms)) # πλήθος δείγματος εκπαίδευσης
train_indices <- sample(seq_len(nrow(sampled_mushrooms)), size = train_size) # δείκτες δείγματος εκπαίδευσης

train_data <- sampled_mushrooms[train_indices, ] # δείγμα εκπαίδευσης
test_data <- sampled_mushrooms[-train_indices, ] # δείγμα ελέγχου

7.1.1 Όλα τα χαρακτηριστικά

Ακολούθως στήνουμε το νευρωνικό δίκτυο με τις προδιαγραφές που επιθυμούμε. Σε αυτή την περίπτωση θα λάβουμε υπ’ όψιν όλα τα Features_N.

modelNetNfull <- nnet(class ~ .,  # όπως και στα rpart() και teain(), έτσι κι εδώ το class ~ . δηλώνει ότι λαμβάνονται υπ' όψιν όλα τα χαρακτηριστικά
               data = train_data,  # Δεδομένα εκπαίδευσης
               size = 1,  # Μόνο 1 νευρώνας στο κρυφό στρώμα (απλό μοντέλο)
               linout = FALSE,  # FALSE για ταξινόμηση. TRUE για πρόβλεψη αριθμών (παλινδρόμηση)
               trace = FALSE)  # FALSE για να μην βγάζει πολλά μηνύματα

# Κάνουμε προβλέψεις στο δοκιμαστικό σύνολο
predictionsNetNfull <- predict(modelNetNfull, newdata = test_data, type = "class")

Ας εξετάσουμε τώρα πόσο καλές προβλέψεις κάνει το μοντέλο μας.

(predictionNet_fullTable <- table(
  Πρόβλεψη = predictionsNetNfull,
  Πραγματική_Τιμή = test_data$class
))
        Πραγματική_Τιμή
Πρόβλεψη    e    p
       e 1137  687
       p  463 1456

Ο παραπάνω πίνακας λέει τα κάτωθι:

  • Διαπιστώθηκαν ορθώς ως εδώδιμα (e) 1137 μανιτάρια.

  • Διαπιστώθηκαν εσφαλμένα ως εδώδιμα (e) 687 μανιτάρια.

  • Διαπιστώθηκαν ορθώς ως δηλητηριώδη (p) 1456 μανιτάρια.

  • Διαπιστώθηκαν εσφαλμένα ως δηλητηριώδη (p) 463 μανιτάρια.

Αυτό σημαίνει ότι είχαμε ακρίβεια:

accuracy_full <- sum(diag(predictionNet_fullTable)) / sum(predictionNet_fullTable)
accuracy_full
[1] 0.6927598

7.1.2 Μόνο τα Feature_2, Feature_1 και Feature_6

Ας εξετάσουμε τώρα τις προβλέψεις που μπορούν να γίνουν εξετάζοντας μόνο τα Feature_2, Feature_1 και Feature_6. Φτιάχνουμε και πάλι το μοντέλο μας.

# Εκπαίδευση του δεύτερου νευρωνικού δικτύου για τα χαρακτηριστικά 2, 1 και 6.
modelNetN.216 <- nnet(class ~ Feature_2 + Feature_1 + Feature_6,  # Μόνο 3 features
               data = train_data,  # Δεδομένα εκπαίδευσης
               size = 1,  # Πάλι 1 νευρώνας
               linout = FALSE,  # FALSE για ταξινόμηση
               trace = FALSE)  # FALSE για ήσυχη εκτέλεση

Ας φτιάξουμε τις προβλέψεις μας.

# Κάνουμε προβλέψεις στο δοκιμαστικό σύνολο
predictionsNetN.216 <- predict(modelNetN.216, newdata = test_data, type = "class")

Και ας δούμε πρακτικά τι καταφέρνει.

# Δημιουργούμε πίνακα σύγχυσης
(predictionsNetN.216.table <- table(Πρόβλεψη = predictionsNetN.216,
                  Πραγματική_τιμή = test_data$class 
                  ))
        Πραγματική_τιμή
Πρόβλεψη    e    p
       e 1083  932
       p  517 1211

Ο παραπάνω πίνακας λέει τα κάτωθι:

  • Διαπιστώθηκαν ορθώς ως εδώδιμα (e) 1083 μανιτάρια.

  • Διαπιστώθηκαν εσφαλμένα ως εδώδιμα (e) 932 μανιτάρια.

  • Διαπιστώθηκαν ορθώς ως δηλητηριώδη (p) 1211 μανιτάρια.

  • Διαπιστώθηκαν εσφαλμένα ως δηλητηριώδη (p) 517 μανιτάρια.

Αυτό σημαίνει ότι είχαμε ακρίβεια:

accuracy_216 <- sum(diag(predictionsNetN.216.table)) / sum(predictionsNetN.216.table)
accuracy_216
[1] 0.6128774

Θυμίζουμε ότι η ακρίβεια όταν εξετάσαμε όλα τα δεδομένα ήταν 0.6927598, ήτοι εμφανώς μεγαλύτερη της 0.6128774 που βρήκαμε τώρα.

7.2 Με caret

Ο γράφων, έχοντας χρησιμοποιήσει σε κάθε μία από τις παραπάνω ενότητες το πακέτο caret σκέφτηκε πως αποτελεί ένα χρήσιμο πακέτο για τη Μηχανική Μάθηση. Επομένως έδωσε και μία απάντηση με τη βοήθεια αυτου΄:

set.seed(student_id)

# Ο έξυπνος Διαχωρισμός που διατηρεί τις αναλογίες στα δείγματα που λαμβάνονται
trainIndex <- createDataPartition(sampled_mushrooms$class, p = 0.75, list = FALSE)
train_set <- sampled_mushrooms[trainIndex, ]
test_set  <- sampled_mushrooms[-trainIndex, ]

ctrl <- trainControl(method = "cv", number = 10) # Ο τρόπος εκπαίδευσης Cross-Validation (10-διαμερίσεις)

# Το caret καλεί την nnet αυτόματα
model_caret.NetN <- train(class ~ ., 
                     data = train_set, 
                     method = "nnet", # εδώ θέλει nnet, πέραν του caret
                     maxit = 1000, # προσπάθειες βελτίωσης
                     trControl = ctrl,
                     tuneGrid = expand.grid(size = 1, decay = 0.1), 
                     # Ορίζουμε το size=1 όπως ζητά η εργασία
                     # decay: Όσο μικρότερο είναι το νούμερο, τόσο πιο πολύ σκαλίζει τις λεπτομέρειες, μο ό,τι αυτό συνεπάγεται για απλοϊκή-πρόχειρη-χοντροκομμένη μελέτη (μεγάλο decay) ή για Overfitting (μικρό decay)
                     # Αν αφαιρεθεί το tuneGrid, η R αποφασίζει μόνη της περί του καλύτερου
                     trace = FALSE,
                     linout = FALSE)

Ας εξτάσουμε και τις προβλέψεις που επιτυγχάνει.

predictionsNetN.caret <- predict(model_caret.NetN, test_set)
resultsNetN.caret <- confusionMatrix(predictionsNetN.caret, test_set$class)
resultsNetN.caret
Confusion Matrix and Statistics

          Reference
Prediction    e    p
         e 1498 1139
         p  160  945
                                          
               Accuracy : 0.6529          
                 95% CI : (0.6374, 0.6681)
    No Information Rate : 0.5569          
    P-Value [Acc > NIR] : < 2.2e-16       
                                          
                  Kappa : 0.3366          
                                          
 Mcnemar's Test P-Value : < 2.2e-16       
                                          
            Sensitivity : 0.9035          
            Specificity : 0.4535          
         Pos Pred Value : 0.5681          
         Neg Pred Value : 0.8552          
             Prevalence : 0.4431          
         Detection Rate : 0.4003          
   Detection Prevalence : 0.7047          
      Balanced Accuracy : 0.6785          
                                          
       'Positive' Class : e

8 Ομαδοποίηση k-μέσων

Η εργασία αφήνει στη ευχέρεια του γράφοντος το αν θα επιλεγεί Elbow Method ή ο Silhouette Score. Προς τούτο έγινε μια υποτυπώδης έρευνα περί του τι είναι καλύτερο και βρέθηκε το εξής από εδώ (μετάφραση ChatGPT):

Πότε να χρησιμοποιήσετε ποια μέθοδο

Χρησιμοποιήστε την Elbow Method όταν:

  • Θέλετε έναν γρήγορο ευρετικό κανόνα για την εκτίμηση του 𝑘.

  • Εργάζεστε με συστάδες χαμηλής διάστασης που διαχωρίζονται καθαρά.

  • Το σύνολο δεδομένων είναι μεγάλο και απαιτείται ταχύτερος υπολογισμός.

Χρησιμοποιήστε την Silhouette Score όταν:

  • Οι συστάδες δεν είναι σαφώς διαχωρίσιμες και υπάρχουν οριακές περιπτώσεις.

  • Θέλετε ένα πιο αντικειμενικό, ποσοτικό κριτήριο.

  • Δέχεστε επιπλέον υπολογιστικό κόστος προκειμένου να επιτύχετε μεγαλύτερη ακρίβεια.

Σε πολλές πρακτικές περιπτώσεις, συνιστάται η ταυτόχρονη χρήση και των δύο μεθόδων:

  • Χρησιμοποιήστε τη Elbow Method για να περιορίσετε ένα μικρό εύρος πιθανών τιμών του 𝑘.

  • Εφαρμόστε την Silhouette Score μέσα σε αυτό το εύρος για να προσδιορίσετε την βέλτιστη τιμή.

Αυτή η υβριδική προσέγγιση διασφαλίζει τόσο την υπολογιστική αποδοτικότητα όσο και την ποιότητα της ομαδοποίησης.

Άλλες πάλι πηγές δηλώνουν ότι ο Silhouette Score υπερέχει γενικώς. Δεδομένου όμως του προβληματισμού που έθεσε η πρώτη πηγή πληροφόρησης, αποφασίστηκε να παρατεθούν κι οι δύο.

Βέβαια, είτε ακολουθήσουμε τη μία μέθοδο, είτε την άλλη, θα πρέπει να πορευτούμε με αριθμητικά δεδομένα. Πέραν του ότι αυτό ζητά η εργασία, είναι και αναγκαίο, διότι οι κατηγορικές μεταβλητές είναι σημεία ενός χώρου που δεν μπορεί να είναι συνεχής. Έτσι λοιπόν:

# Μόνο τα Feature_7", "Feature_6", "Feature_1" ήταν αριθμητικά
sampled_mushrooms_numeric <- sampled_mushrooms[, c("Feature_7", "Feature_6", "Feature_1")]

Ακολούθως κανονικοποιούμε τα δεδομένα μας, ώστε να μην δίνεται περισσότερη βαρύτητα στα Features με μεγαλύτερες τιμές.

sampled_mushrooms_scaled <- as.data.frame(scale(sampled_mushrooms_numeric))

8.1 Elbow Method

Η μέθοδος \(k\)-μέσων συνίσταται στο να εντοπίσουμε \(k\) συστάδες, όπου αν πάρουμε τις αποστάσεις των σημείων της κάθε μίας από τα κέντρα τους, συνολικά αυτές να έχουν τη μικρότερη δυνατή τιμή. Με άλλα λόγια, θέλουμε αυτά τα \(k\) μέσα να είναι όσο το δυνατόν πιο αντιπροσωπευτικά της κάθε συστάδας. Η εν λόγω απόσταση ονομάζεται WSS.

Μεγαλώνοντας το \(k\) η WSS μειώνεται, συνεπώς θα κρατήσουμε το \(k\), όπου από κει και πέρα η WSS αρχίσει και σταθεροποιείται.

Αρχικά, βέβαια, αρχικοποιούμε τη λίστα με τις τιμές της WSS που θα προκύψουν. Επειδή θα εξετάσουμε τα παραπάνω για την περίπτωση μίας συστάδας, δύο συστάδων, …, δέκα συστάδων, δημιουργούμε αρχικά ένα διάνυσμα με \(10\) μηδενικά.

wss <- numeric(10)

Προχωράμε σε αυτούς τους \(10\) υπολογισμούς των WSS.

for (k in 1:10) {
  kmeans_model <- kmeans(sampled_mushrooms_scaled, 
                       centers = k, # πόσες συστάδες/κέντρα
                       nstart = 20, # πόσες αρχικοποιήσεις/επανεκκινήσεις της διαδικασίας
                       iter.max = 100 # πόσες επαναλήψεις βελτίωσης θα γίνουν μέσα στην διαδικασία, μέχρι να βρεθούν (υποψιαστούμε) τα κέντρα
                       )
  wss[k] <- kmeans_model$tot.withinss # Επικαιροποίηση της κ συνιστώσας του wss.
}
Warning: Quick-TRANSfer stage steps exceeded maximum (= 748600)
Warning: Quick-TRANSfer stage steps exceeded maximum (= 748600)
Warning: Quick-TRANSfer stage steps exceeded maximum (= 748600)

Οι τιμές που βγάλαμε για τα διάφορα \(k\) είναι οι παρακάτω.

data.frame(k = 1:10, WSS = wss)
    k       WSS
1   1 44913.000
2   2 26461.620
3   3 20482.934
4   4 16735.409
5   5 13829.113
6   6 11455.686
7   7  9724.406
8   8  8526.080
9   9  7742.080
10 10  7131.578

Βλέπουμε αυτό που λέγαμε αρχικά, ότι δηλαδή μεγαλώνοντας το \(k\) επιτυγχάνεται η μείωση της WSS. Η Elbow method συνίσταται στο να δούμε γραφικά σε ποιο \(k\) η WSS αποκτάει μια «μόνιμη» χαμηλή τιμή.

plot(1:10, wss,
     type = "b", 
     xlab = "k",
     ylab = "WSS",
     main = "Elbow Method")

«Με το μάτι» κρίνοντας φαίνεται ότι μετά από τις 2 συστάδες (\(k>2\)) η WSS παύει να πέφτει τόσο απότομα. Διαλέγουμε, λοιπόν, \(k=2\) και εφαρμόζουμε τον αλγόριθμο ομαδοποίησης πάνω στα δεομένα μας.

optimal_k <- 2

set.seed(student_id)
final_clusters <- kmeans(sampled_mushrooms_scaled, centers = optimal_k, nstart = 25, iter.max = 100)

Ακολούθως μπορούμε να δούμε πόσα στοιχεία ανήκουν σε κάθε μία από τις τρεις συστάδες.

final_clusters$size
[1]  4745 10227

Τέλος, επικαιροποιούμε τον πίνακα sampled_mushrooms, ώστε να συμπεριλαμβάνει την ομαδοποίηση που επιτύχαμε.

sampled_mushrooms$cluster_id <- as.factor(final_clusters$cluster)
knitr::kable(head(sampled_mushrooms)) %>%
  kable_styling("striped", full_width = T) %>%
  scroll_box(width = "100%", height = "max-content")
class Feature_7 Feature_11 Feature_6 Feature_2 Feature_10 Feature_8 Feature_1 Feature_5 Feature_4 cluster_id
40828 p 25.02 u 14.69 x d y 12.49 o FALSE 1
26825 p 26.70 a 6.68 f d w 18.91 w TRUE 1
9321 e 3.14 a 4.92 b g y 3.04 w FALSE 2
15313 p 12.79 a 4.35 x d w 5.11 w TRUE 2
3074 e 20.14 u 27.41 f d n 18.98 w FALSE 1
38361 p 5.18 a 5.05 x d e 3.54 e FALSE 2 
# Δημιουργία του 3D γραφήματος
plot_ly(
  data = sampled_mushrooms,       # Ορίζουμε το data frame που περιέχει τα δεδομένα μας
  x = ~Feature_7,                # Ορισμός του άξονα Χ
  y = ~Feature_6,                # Ορισμός του άξονα Υ
  z = ~Feature_1,                # Ορισμός του άξονα Z
  
  color = ~cluster_id,           # Διαχωρισμός χρωμάτων με βάση την συστάδα που ανήκει το εκάστοτε σημείο
  colors = "Set1",             # Επιλογή συγκεκριμένης χρωματικής παλέτας (βλ. https://plotly.com/python/discrete-color/)
  
  type = "scatter3d",            # Καθορισμός του τύπου γραφήματος ως 3D Διάγραμμα Διασποράς
  mode = "markers",               # Εμφάνιση μόνο σημείων (τελείες) χωρίς να ενώνονται με γραμμές
  
  marker = list(                 # Ρυθμίσεις για την εμφάνιση των σημείων:
    size = 3,                    # Καθορισμός μεγέθους της κάθε τελείας
    opacity = 0.8                # Καθορισμός διαφάνειας 
  )
) %>% 
  layout(                        # Ρυθμίσεις για τη συνολική εμφάνιση και τους τίτλους
    title = "3D Οπτικοποίηση των συστάδων", # Ο τίτλος του γραφήματος
    
    scene = list(                # Ρυθμίσεις για το 3D περιβάλλον (σκηνή)
      xaxis = list(title = 'Feature 7'), # Ονομασία του άξονα Χ
      yaxis = list(title = 'Feature 6'), # Ονομασία του άξονα Υ
      zaxis = list(title = 'Feature 1')  # Ονομασία του άξονα Ζ
    )
  )

Ο γράφων οφείλει να ομολογήσει πως το παραπάνω γράφημα ήταν μια απογοήτευση. Αντί να χρωματιστούν οι συστάδες που φαίνεται να υπάρχουν, ο αλγόριθμος απλά πήρε ένα μαχαίρι κι έκοψε σε δυο φέτες το σημειοσύνολο. Σε σχετική ερώτηση προς το Gemini πήρε την απάντηση ότι αυτό είναι απόλυτα φυσιολογικό. Ομοίως απήντησαν κι άλλα LLM, όπως το ChatGPT και το DeepSeek, τα οποία έθεσαν και το ζήτημα του ότι απεικονίζω τα μη-κανονικοποιημένα δεδομένα.

Όμως και η απεικόνιση των κανονικοποιημένων δεδομένων οδηγεί στα ίδια παράλογα (με το μάτι) αποτελέσματα, συνεπώς, βάζουμε μια άνω τελεία στην εν λόγω μελέτη και προχωράμε να δούμε την απόδοση και των υπολοίπων.

Κλείνοντας, αξίζει ίσως να αναφερθεί ότι τα βήματα υπολογισμού των WSS βάσει των διαφόρων \(k\) μπορούν να απλοποιηθούν μέσω της συνάρτησης fviz_nbclust() του πακέτου factoextra, χρησιμοποιώντας συχρόνως το πακέτο cluster (βλ. οδηγίες εδώ). Επειδή, όμως η fviz_nbclust() φαίνεται να είναι αρκετά βαριά, θα αρκεστούμε στην εξέταση ενός δείγματος του sampled_mushrooms_scaled.

set.seed(student_id) 
s.m.s_sample <- sampled_mushrooms_scaled[sample(1:nrow(sampled_mushrooms_scaled), 1000), ]
fviz_nbclust(s.m.s_sample, kmeans, method = "wss", nstart = 10, iter.max = 100)

8.2 Silhouette Score

Στην παρούσα μέθοδο οι συστάδες προσδιορίζονται πάλι με τον αλγόριθμο k-means, απλά το ιδανικό πλήθος συστάδων προσδιορίζεται με άλλον τρόπο. Συγκεκριμένα, αντί ο στόχος να είναι η εξομάλυνση της WSS, στόχος είναι να μεγιστοποιηθεί η μέση απόσταση των κλάσεων μεταξύ τους.

Η εν λόγω απόστση είναι αυτό που αποκαλούμε Silhouette Score. Συγκεκριμένα, παίρνει τιμές από -1 έως 1, όπου (βλ. εδώ):

  • Οι θετικές τιμές υποδηλώνουν ότι τα σημεία δεδομένων ανήκουν στις σωστές συστάδες, γεγονός που δείχνει καλά αποτελέσματα ομαδοποίησης.

  • Μια τιμή ίση με μηδέν υποδηλώνει επικαλυπτόμενες συστάδες ή σημεία δεδομένων που βρίσκονται σε ίση απόσταση από περισσότερες από μία συστάδες.

  • Οι αρνητικές τιμές υποδηλώνουν ότι τα σημεία δεδομένων έχουν ανατεθεί σε λανθασμένες συστάδες, γεγονός που δείχνει κακά αποτελέσματα ομαδοποίησης.

Επειδή ο υπολογισμός του Silhouette Score απαιτεί τον υπολογισμό της απόστασης κάθε σημείου από κάθε άλλο, είναι υπολογιστικά δαπανηρός, θα αρκεστούμε στον υπολογισμό του από ένα τυχαίο δείγμα του. Έτσι, αφού η χρήση δείγματος καθίσταται μονόδρομος, μπορούμε να χρησιμοποιήσουμε τη συνάρτηση fviz_nbclust, με τον τρόπο που συστήνεται εδώ

fviz_nbclust(s.m.s_sample, kmeans, method = "silhouette")

Και αυτή η μέθοδος, όπως η elbow, δίνει δύο συστάδες. Δεδομένου ότι η διαδικασία διαφοροποιείται μόνο ως προς το πόσες είναι οι ομάδες μας, δεν έχουμε τίποτα καινούριο να συναντήσουμε εδώ σε σχέση με αυτά που γράψαμε και απεικονίσαμε στην υποενότητα για τη μέθοδο Elbow. Συνεπώς μπορούμε να παραλείψουμε τις επαναλήψεις και να προχωρήσουμε στην επόμενη ενότητα.

9 Hierarchical Clustering

Αρχικά κάνουμε την τυχαία δειγματοληψία που ζητάει η εργασία.

set.seed(student_id)  
sampled_data <- sampled_mushrooms[
  sample(nrow(sampled_mushrooms), 1000),
]

Εν συνεχία επιλέγουμε δύο αριθμητικά χαρακτηριστικά του δείγματός μας.

numeric_features <- sampled_data[, c("Feature_7", "Feature_6")]

Τέλος, κανονικοποιούμε το dataframe που σχηματίστηκε:

scaled_features <- scale(numeric_features)

Έτσι, είμαστε έτοιμοι να φτιάξουμε τη μήτρα απόστασης:

distance_matrix <- dist(
  scaled_features,
  method = "manhattan"
)

Έτσι είναι έτοιμη να αρχίσει η διαδικασία του Hierarchical clustering.

HierarchicalClustering <- hclust(
  distance_matrix,
  method = "complete"
)

Ας δούμε το δεντρόγραμμα που προκύπτει.

plot(
  HierarchicalClustering,
  labels = FALSE,
  main = "Δεντρόγραμμα - Hierarchical Clustering",
  xlab = "είδος μανιταριού",
  ylab = "Manhattan distance"
)

«Με το μάτι» βλέπουμε ότι υπάρχουν δύο βασικές ομάδες. Μία μικρή ομάδα από λίγα στοιχεία στρημωγμένα στα αριστερά και μια τεράστια ομάδα με πλήθος υπο-ομάδων δεξιά αυτής. Θα χωρίσουμε το sampled_data στις δύο αυτές ομάδες.

clusters <- cutree(HierarchicalClustering, k = 2)

Ακολούθως εφοδιάζουμε το sampled_data με την πληροφορία περί του αν το εκάστοτε μανητάρι ανήκει στη μία ή την άλλη ομάδα.

sampled_data$cluster_result <- as.factor(clusters)

Και τώρα ας δούμε τι έχουμε καταφέρει βλέποντας την διαμέριση των σημείων που επιτυγχάνεται στον χώρο Feature_7\(\times\)Feature_6.

ggplot(sampled_data, aes(x = Feature_7, y = Feature_6, color = cluster_result)) +
  geom_point(alpha = 0.6) +
  labs(title = "Οπτικοποίηση ομάδων",
       x = "Feature 7", y = "Feature 6",
       color = "Ομάδα") +
  theme_minimal()

10 DBSCAN

10.1 Με δεδομένα εργασίας

Καταρχάς, θα αποφύγουμε την κανονικοποίηση ακολουθώντας τις συμβουλές της απάντησης αυτής (μετάφραση Gemini):

Η κανονικοποίηση ή η τυποποίηση των δεδομένων σας μπορεί να καταστρέψει σημαντικές ιδιότητες του συνόλου δεδομένων σας.

Ορισμένα παραδείγματα:

  • Τα δεδομένα σας είναι γεωγραφικές συντεταγμένες: Το γεωγραφικό πλάτος και το γεωγραφικό μήκος δεν πρέπει ποτέ να κανονικοποιούνται ή να τυποποιούνται.

  • Τα δεδομένα σας είναι ιστογράμματα: Η μόνη ουσιαστική κανονικοποίηση είναι να κάνετε το άθροισμα του ιστογράμματος ίσο με 1. Ποτέ μην μετασχηματίζετε μεμονωμένες μεταβλητές!

  • Τα δεδομένα σας έχουν ένα ουσιαστικό μηδέν: Για παράδειγμα, αν πρόκειται για μια χρηματική αξία. Ο μετασχηματισμός με \(sgn(x) \cdot \sqrt{|x|}\) μπορεί να είναι χρήσιμος σε ορισμένους τομείς πάντως.

  • Τα δεδομένα σας είναι αραιά (sparse): Ποτέ μην κάνετε τυποποίηση. (Η κανονικοποίηση μπορεί να είναι «εντάξει» αν δεν έχετε αρνητικές τιμές).

Η επιλογή της κλιμάκωσης (scaling) δεν πρέπει να γίνεται «επειδή γίνεται πάντα», αλλά βάσει των πραγματικών δεδομένων που έχετε! Επιλέξτε την επειδή είναι το σωστό, όχι επειδή είναι η «προεπιλογή» ή επειδή το είδατε σε κάποιο σεμινάριο.

Πιθανότατα, αν καταφεύγετε στην κανονικοποίηση ή την τυποποίηση χωρίς σκέψη, σημαίνει ότι δεν έχετε κατανοήσει τα δεδομένα σας, ούτε το πώς να μετρήσετε την απόσταση ή την ομοιότητα. Πολλοί χρησιμοποιούν την κανονικοποίηση ως έσχατη λύση για να πάρουν «κάποιο» αποτέλεσμα, αλλά ποτέ δεν μπορείτε να είστε σίγουροι αν το αποτέλεσμα αυτό έχει όντως νόημα.

Δεδομένου ότι εδώ δεν έχουμε εικόνα περί του τι είναι τα χαρακτηριστικά των μανηταριών που μελετάμε, θα αποφύγουμε την κανονικοποίηση/κλιμάκωση.

# Εκτέλεση DBSCAN με τις παραμέτρους της εργασίας
db1 <- dbscan(numeric_features,# τα δεδομένα
              eps = 0.5, # η ακτίνα (ε) της περιοχής αντός της οποίας τα σημεία ορίζονται ως γειτονικά του κέντρου της
              minPts = 2 # πλήθος σημείων όπου αν υπάρχουν εντός της Β(ε) έχουμε πυκνή περιοχή.
              )

Ας δούμε τις ομάδες που σχηματίζει η DBSCAN.

unique(db1$cluster)
 [1]  1  2  3  4  5  6  0  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24
[26] 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49
[51] 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74
[76] 75 76 77 78

Βλέπουμε ότι σχηματίστηκαν 79 ομάδες. Δεδομένου ότι το 0 αντιπροσωπεύει τον θόρυβο, θα μπορούσαμε να πούμε ότι ουσιαστικά είναι 78 ομάδες. Θα λέγαμε ότι είναι αρκετές, αλλά εν πάση περιπτώσει, ας επικαιροποιήσουμε το dataframe μας με την ομαδοποίηση που πετύχαμε.

numeric_features1 <- numeric_features
numeric_features1$ClusterDbscan <- as.factor(db1$cluster)
head(numeric_features1)
      Feature_7 Feature_6 ClusterDbscan
43564     12.86     12.04             1
28112      8.99      5.78             2
45632      3.61      5.68             2
56782      0.00      0.00             3
45485      3.63      6.46             2
7029       7.18      2.72             4

Κι ας δούμε σχηματικά τα πεπραγμένα μας.

ggplot(
  numeric_features1,
  aes(x = Feature_7, y = Feature_6, color = ClusterDbscan)
) +
  geom_point(size = 2, alpha = 0.8) +
  labs(
    title = "DBSCAN (eps = 0.5, minPts = 2)",
    x = "Feature_7",
    y = "Feature_6",
    color = "Ομάδα"
  )

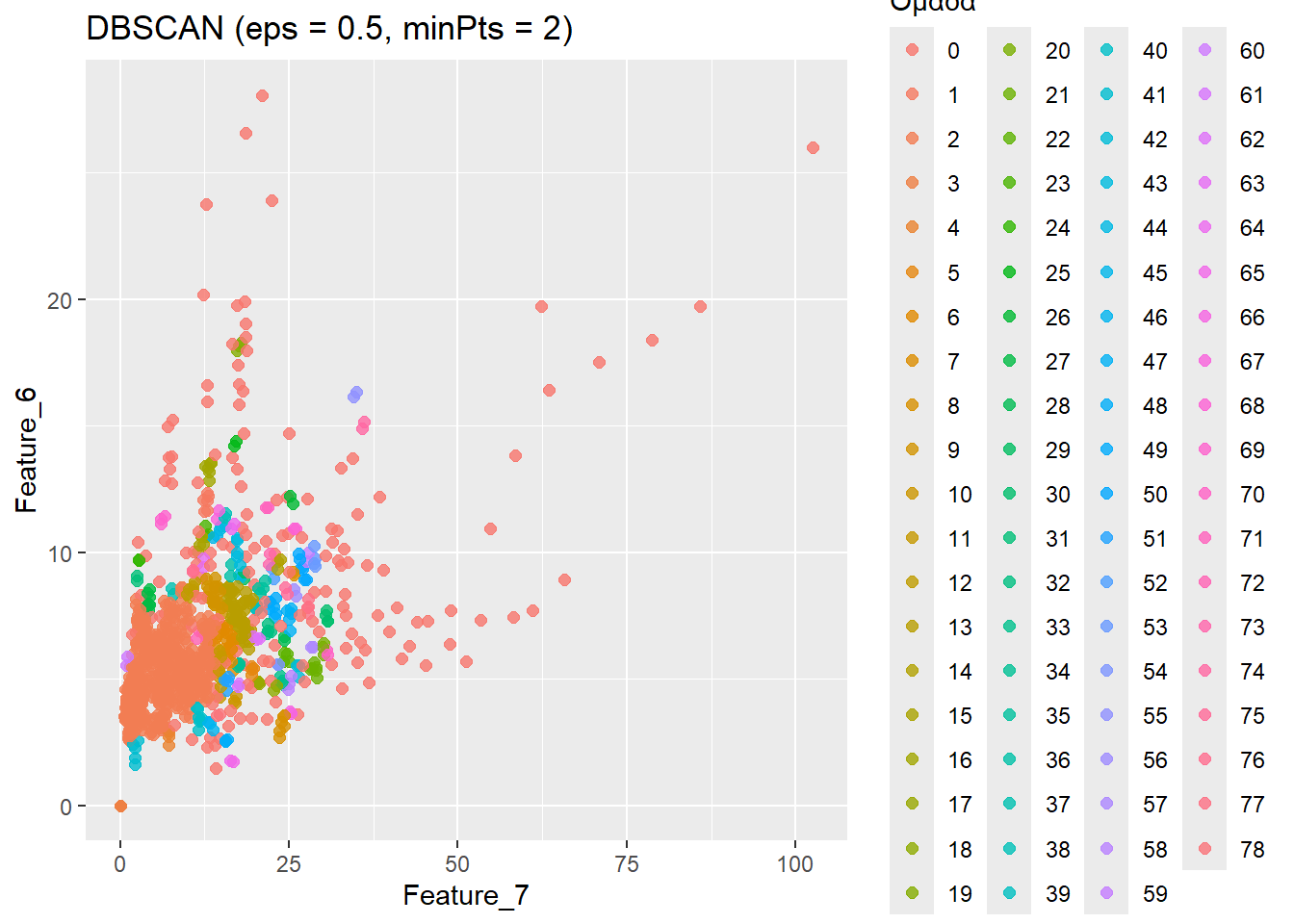
Ο γράφων οφείλει να ομολογήσει ότι δεν έμεινε ιδιέτερα ικανοποιημένος από τα αποτελέσματα αυτά, συνεπώς έψαξε πληροφορίες για τις παραμέτρους eps και minPts. Τα αποτελέσματα ακολουθούν στην επόμενη ενότητα.

10.2 Με προτεινόμενα eps και minPts

Σύμφωνα με αυτή και αυτή την πηγή, το minPts είναι εν γένει χρήσιμο να τίθεται ίσο με το διπλάσιο της διάστασης του πίνακά μας. Εν προκειμένω, αφού έχουμε δύο Features θα πρέπει minPts=4. Η ίδια πηγή αναφέρει ότι για να προσδιοριστεί το eps θα πρέπει να εφαρμοσουμε k-NN, να σχεδιάσουμε το k-NN distance plot και να βρούμε την k-απόσταση που παρατηρείται «αγκώνας» στο γράφημα. Αυτή τελικά θα τη θέσουμε ως eps.

kNNdistplot(numeric_features, minPts=4)

Βλέπουμε ότι ο «αγκώνας» είναι κάπου ανάμεσα στο 800 και το 1000, οπότε ζουμάρουμε.

# Υπολογισμός των αποστάσεων
dist_values <- kNNdist(numeric_features, k = 4)

# Ταξινόμηση των αποστάσεων σε αύξουσα σειρά
dist_values_sorted <- sort(dist_values)


# Δημιουργία γραφήματος με Zoom
plot(dist_values_sorted, type = "l", col = "blue", lwd = 2,
     main = "K-distance Graph",
     xlab = "Points (sorted by distance)", 
     ylab = "ε",
     xlim = c(880, 920), # Zoom στο τέλος της καμπύλης
     ylim = c(1, 1.5)) # Zoom στον άξονα y

# Προσθήκη πλέγματος
grid(nx = NULL, ny = NULL, col = "gray", lty = "dotted")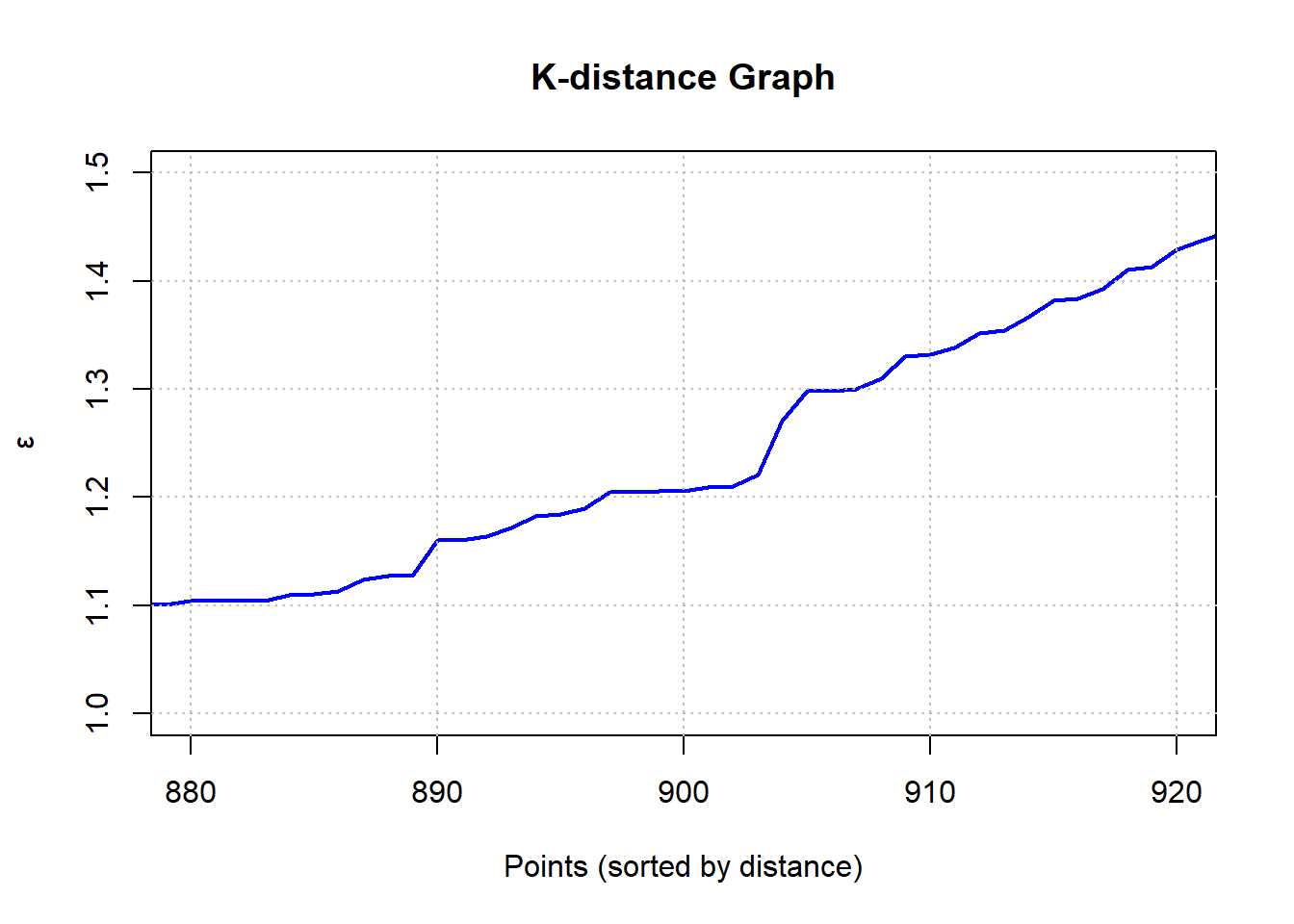

Από το σχήμα διαπιστώνουμε ότι μάλλον eps=1.3, οπότε προχωράμε με αυτή την τιμή και με minPts = 4, όπως προαναφέραμε.

# Εκτέλεση DBSCAN με τις παραμέτρους που βρήκαμε
db2 <- dbscan(numeric_features,# τα δεδομένα
              eps = 1.3, # η ακτίνα (ε) της περιοχής αντός της οποίας τα σημεία ορίζονται ως γειτονικά του κέντρου της
              minPts = 4 # πλήθος σημείων όπου αν υπάρχουν εντός της Β(ε) έχουμε πυκνή περιοχή.
              )

Ας δούμε και τις ομαδοποιήσεις που προκύπτουν.

unique(db2$cluster)
[1] 1 2 4 3 0 5 6

Προκύπτουν 79 ομάδες, ήτοι 78 χωρίς τα απομωνομένα σημεία. Σαφώς καλύτερα από πριν.

Να επικαιροποιήσουμε και το dataframe μας.

numeric_features2 <- numeric_features
numeric_features2$ClusterDbscan <- as.factor(db2$cluster)
head(numeric_features2)
      Feature_7 Feature_6 ClusterDbscan
43564     12.86     12.04             1
28112      8.99      5.78             1
45632      3.61      5.68             1
56782      0.00      0.00             2
45485      3.63      6.46             1
7029       7.18      2.72             1

Και ας εξετάσουμε και σχηματικά τη νέα αυτή προσέγγιση.

ggplot(
  numeric_features2,
  aes(x = Feature_7, y = Feature_6, color = ClusterDbscan)
) +
  geom_point(size = 2, alpha = 0.8) +
  labs(
    title = "DBSCAN (eps = 1.3, minPts = 4)",
    x = "Feature_7",
    y = "Feature_6",
    color = "Ομάδα"
  )

11 Αναφορές

11.1 Ιστοσελίδες

  1. ggpairs(): Pairwise plot matrix

  2. Identify and Remove Duplicate Data in R

  3. Decision Trees - VisuallyExplained

  4. Decision Tree: Important things to know

  5. Decision Tree in R Programming

  6. Hold-out vs. Cross-validation in Machine Learning

  7. Elbow Method vs Silhouette Co-efficient in Determining the Number of Clusters

  8. Elbow Method vs. Silhouette Score: which is better?

  9. K Means

  10. K means Clustering – Introduction

  11. How to Use the Elbow Method in R to Find Optimal Clusters

  12. Silhouette Algorithm to determine the optimal value of k

  13. What is Silhouette Score?

  14. R Series — K means Clustering (Silhouette)

  15. DBSCAN in R

  16. A Guide to the DBSCAN Clustering Algorithm

  17. Random forests two ways

  18. Ranger Function In R

  19. Random forest and bootstrap

11.2 Συγγράμματα

  1. Hands-On Machine Learning with R. Brad Boehmke & Brandon Greenwell. CRC Press, 2020.

  2. Introduction to Machine Learning with R. Burger Scott. O’Reilly Media, 2018.

  3. Προγραμματισμός σε R για την επιστήμη των δεδομένων. Hadley Wickham & Garret Grolemund. Κλειδάριθμος, 2022.

  4. Στατιστική, ανάλυση δεδομένων με τη χρήση της R. Robert S. Wiee, John S. Witte, Γιώργος Ανδρουλάκης & Κωνσταντίνος Κουνετάς. Κριτική, 2019.

  5. Practical Machine Learning with R. Carsten Lange. CRC Press, 2024

  6. Μηχανική Μάθηση. Κωνσταντίνος Διαμαντάρας & Δημήτρης Μπότσης. Κλειδάριθμος, 2019.